1.1 Two basic rules

Quantum theory, at least at some instrumental level, can be viewed as a modification of probability theory: we replace positive real numbers (i.e. probabilities) with complex numbers z, called probability amplitudes (or simply “amplitudes”), such that the squares of their absolute values |z|^2 are interpreted as probabilities.

The correspondence between probability amplitudes z and probabilities |z|^2 is known as Born’s rule, named for physicist and mathematician Max Born (1882–1970).

The rules for combining amplitudes are very reminiscent of the rules for combining probabilities:

  1. Whenever something can happen in a sequence of independent steps, we multiply the amplitudes of each step.

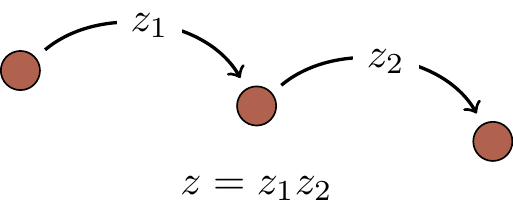
  1. Whenever something can happen in several alternative ways, we add the amplitudes for each separate way.

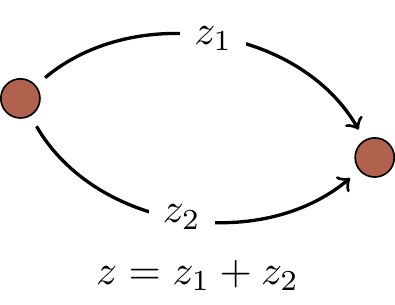
That’s it! These two rules are basically all you need to manipulate amplitudes in any physical process, no matter how complicated.23 They are universal and apply to any physical system, from elementary particles through atoms and molecules to white dwarfs stars. They also apply to information, since, as we have already emphasised, information is physical. The two rules look deceptively simple but, as you will see in a moment, their consequences are anything but trivial.

  1. We will, however, amend the two rules later on when we touch upon particle statistics.↩︎