Composition of rotations
We are now in a position to understand the circuit in Figure 2.3 in geometric terms.
It is a very useful fact of geometry (which we shall take for granted) that any rotation in three-dimensional Euclidean space can be performed as a sequence of three specific rotations: one about the z-axis, one about the x-axis, and one more about z-axis.
The circuit does exactly this:
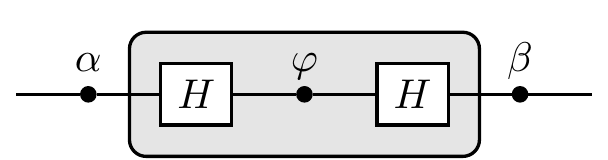
The first phase gate effects rotation by \alpha about the z-axis, the second phase gate is sandwiched between the two Hadamard gates, and these three gates together effect rotation by \varphi about the x-axis, and, finally, the third phase gates effects rotation by \beta about the z-axis.
So we can implement any unitary U by choosing the three phase shifts, \alpha, \varphi, and \beta, which are known as the three Euler angles.
