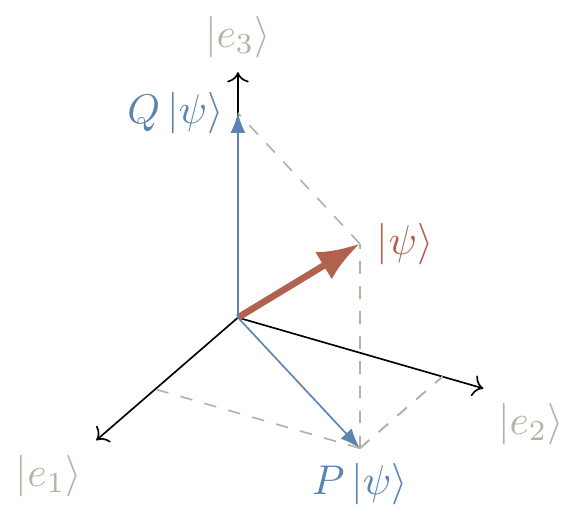
Example of an incomplete measurement
Take a three-dimensional Hilbert space \mathcal{H} with basis \{|e_1\rangle,|e_2\rangle,|e_3\rangle\}, and consider the two orthogonal projectors
\begin{aligned}
P &= |e_1\rangle\langle e_1| + |e_2\rangle\langle e_2|
\\Q &= |e_3\rangle\langle e_3|
\end{aligned}
These form the decomposition of the identity: P+Q=\mathbf{1}.
Now suppose that a physical system is prepared in state |\psi\rangle = \alpha_1|e_1\rangle + \alpha_2|e_2\rangle + \alpha_3|e_3\rangle.
Ideally, we would like to perform a complete measurement that would resolve the state |\psi\rangle into the three basis states, but suppose our experimental apparatus is not good enough, and lumps together |e_1\rangle and |e_2\rangle.
In other words, it can only differentiate between the two subspaces associated with projectors P and Q.
The apparatus, in this incomplete measurement, may find the system in the subspace associated with P.
This happens with probability
\begin{aligned}
\langle\psi|P|\psi\rangle
&= \langle\psi|e_1\rangle \langle e_1|\psi\rangle + \langle\psi|e_2\rangle \langle e_2|\psi\rangle
\\&= |\alpha_1|^2 + |\alpha_2|^2,
\end{aligned}
and the state right after the measurement is the normalised vector P|\psi\rangle, i.e.
\frac{\alpha_1|e_1\rangle+\alpha_2|e_2\rangle}{\sqrt{|\alpha_1|^2 + |\alpha_2|^2}}.
The measurement may also find the system in the subspace associated with Q with the probability \langle\psi|Q|\psi\rangle = |\alpha_3|^2, resulting in the post-measurement state |e_3\rangle.