How far apart are two quantum states?
Given two pure states, |u\rangle and |v\rangle, we could try to measure the distance between them using the Euclidean distance \|u-v\|.
This works for vectors, but has some drawbacks when it comes to quantum states.
Recall that a quantum state is not represented by just a unit vector, but by a ray, i.e. a unit vector times an arbitrary phase factor.
Multiplying a state vector by an overall phase factor has no physical effect: the two unit vectors |u\rangle and e^{i\phi}|u\rangle describe the same state.
So, in particular, we want the distance between |u\rangle and -|u\rangle to be zero, since these describe the same quantum state.
But if we were to use the Euclidean distance, then we would have that \|u-(-u)\|=\|u+u\|=2, which is actually as far apart as the two unit vectors can be!
One solution to this problem is to define the distance between |u\rangle and |v\rangle as the minimum over all phase factors, i.e.
d(u,v)\coloneqq \min_{\phi\in[0,2\pi)}\Big\{\|u-e^{i\phi}v\|\Big\}.
But with some algebraic manipulation we can actually figure out what this minimum is without calculating any of the other values.
We first express the square of the distance between any two vectors in terms of their inner product:
\begin{aligned}
\|u-v\|^2
&= \langle u-v|u-v\rangle
\\&= \langle u|u\rangle - \langle u|v\rangle - \langle v|u\rangle + \langle v|v\rangle
\\&= \|u\|^2 +\|v\|^2 - 2\operatorname{Re}\langle u|v\rangle
\end{aligned}
(where \operatorname{Re}(z) is the real part of the complex number z).
Then we can write the Euclidean distance between state vectors as
\|u-v\| = \sqrt{2(1-\operatorname{Re}\langle u|v\rangle)}.
Now if we want to minimise this expression over all rotations of v, then we want \langle u|v\rangle to be real and as large as possible, i.e. for \langle u|v\rangle=|\langle u|v\rangle|.
This gives us a definition of distance.
The state distance between two state vectors |u\rangle and |v\rangle is
d(u,v) \coloneqq \sqrt{2(1-|\langle u|v\rangle|)}.
Note that we sometimes write the state distance as \|u-v\|, and we might refer to it as “Euclidean distance”, which is an abuse of notation: really we should be writing \min\{\||u\rangle-e^{i\varphi}|v\rangle\|\}.
But this sort of thing happens a lot in mathematics, and it’s good to get used to it.
The justification is that, as we have already said, the usual Euclidean distance doesn’t really make great sense for state vectors (because of this vector vs. ray distinction), and so if we know that |u\rangle and |v\rangle are state vectors then writing \|u-v\| (which is already shorthand for \||u\rangle-|v\rangle\|) should suggest “oh, they mean the version of \|\cdot\| that makes sense for state vectors, where we take a minimum”.
For small values of d(u,v)=\|u-v\|, we can think of this distance as being the angle between the two unit vectors.
Indeed, if we think of Euclidean (unit) vectors, then the difference v-u is, for sufficiently small \|u-v\|, just the angle between the two unit vectors (expressed in radians), because a small segment of a circle “almost” looks like a triangle.
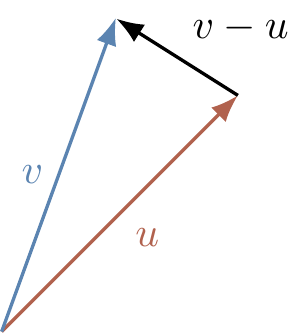
Alternatively (and more formally), we can see this by writing |\langle u|v\rangle|=\cos\alpha\approx1-\alpha^2/2, since then
\|u-v\|
= \sqrt{2(1-|\langle u|v\rangle|)}
\approx \alpha.
This can certainly help with intuition, but extra care must always be taken when dealing with complex vector spaces, since our geometric intuition breaks down rapidly in (complex) dimension higher than 1.
As you might hope, two state vectors which are close to one another give similar statistical predictions.
In order to see this, pick a measurement (any measurement) and consider one partial outcome described by a projector |a\rangle\langle a|.
What can we say about the difference between the two probabilities
\begin{aligned}
p_u &= |\langle a|u\rangle|^2
\\p_v &= |\langle a|v\rangle|^2
\end{aligned}
if we know that \|u-v\|\leqslant\varepsilon?
Well, first of all, let us introduce two classic tricks that are almost always useful when dealing with inequalities — the first holds in any normed vector space, and the latter in any inner product space.
- the reverse triangle inequality:
\Big|\|u\|-\|v\|\Big| \leqslant\|u-v\|
- the Cauchy–Schwartz inequality:
\langle u|v\rangle^2 \leqslant\langle u|u\rangle\langle v|v\rangle
or, equivalently (by taking square roots),
|\langle u|v\rangle| \leqslant\|u\|\|v\|.
Furthermore, the two sides of the inequality are equal if and only if |u\rangle and |v\rangle are linearly dependent.
Using these, we see that
\begin{aligned}
|p_u-p_v|
&= \Big| |\langle a|u\rangle|^2 - |\langle a|v\rangle|^2 \Big|
\\&= \Big| \Big( |\langle a|u\rangle| + |\langle a|v\rangle| \Big) \Big( |\langle a|u\rangle| - |\langle a|v\rangle| \Big) \Big|
\\&\leqslant 2\Big| |\langle a|u\rangle| - |\langle a|v\rangle| \Big|
\\&\leqslant 2\Big| \langle a|u\rangle - \langle a|v\rangle \Big|
\\&\leqslant 2\|a\|\|u-v\|
\\&= 2\|u-v\|.
\end{aligned}
So if \|u-v\|\leqslant\varepsilon, then |p_u-p_v|\leqslant 2\varepsilon.
Again, we can appeal to some geometric intuition if we pretend that |u\rangle and |v\rangle are Euclidean vectors instead of rays.
Write
\begin{aligned}
|\langle a|u\rangle| &= \cos(\alpha)
\\|\langle a|v\rangle| &= \cos(\alpha+\varepsilon)
\end{aligned}
where \varepsilon is the (very small) angle between |u\rangle and |v\rangle, whence \|u-v\|=\varepsilon.
Then
\begin{aligned}
|\langle a|u\rangle|^2 - |\langle a|v\rangle|^2
&= \cos^2(\alpha) - \cos^2(\alpha+\varepsilon)
\\&\approx \varepsilon\sin(2\alpha)
\\&\leqslant\varepsilon.
\end{aligned}
As an interesting exercise, you might try to explain why this approach gives a tighter bound (\varepsilon instead of 2\varepsilon).
