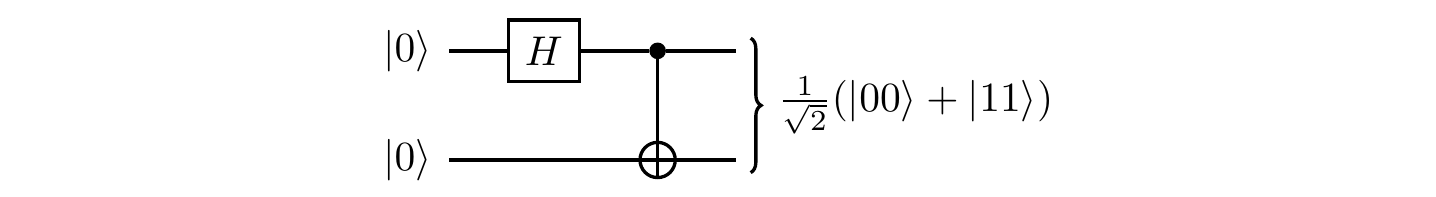Bell states
We start with the generation of entanglement.
Here is a simple circuit that demonstrates the entangling power of \texttt{c-NOT}:
(Generating entanglement).
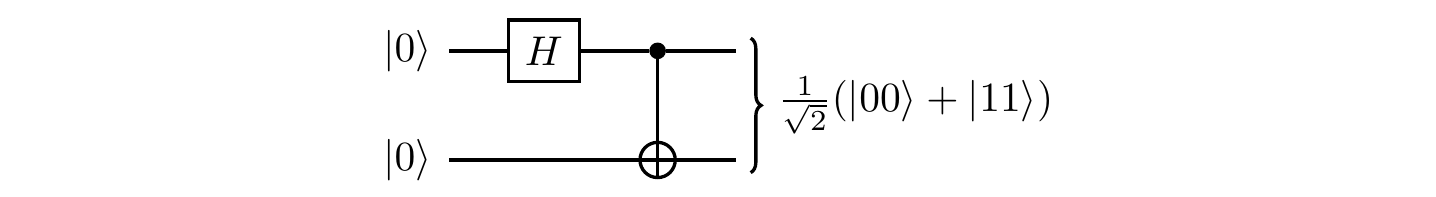
In this circuit, the separable input |0\rangle|0\rangle evolves as
\begin{aligned}
|0\rangle|0\rangle
\overset{H}{\longmapsto}& \frac{1}{\sqrt{2}} (|0\rangle + |1\rangle) |0\rangle
\\=& \frac{1}{\sqrt{2}}|0\rangle|0\rangle + \frac{1}{\sqrt{2}}|1\rangle|0\rangle
\\\overset{\texttt{c-NOT}}{\longmapsto}& \frac{1}{\sqrt{2}}|0\rangle|0\rangle + \frac{1}{\sqrt{2}}|1\rangle|1\rangle
\end{aligned}
resulting in the entangled output \frac{1}{\sqrt{2}}(|00\rangle+|11\rangle).
In fact, this circuit implements the unitary operation which maps the standard computational basis into the four entangled states, known as the Bell states.
The Bell states |\psi_{ij}\rangle are those generated by the above circuit:
\begin{aligned}
|00\rangle
&\longmapsto
|\psi_{00}\rangle \coloneqq \frac{1}{\sqrt{2}}(|00\rangle+|11\rangle)
\\|01\rangle
&\longmapsto
|\psi_{01}\rangle \coloneqq \frac{1}{\sqrt{2}}(|01\rangle+|10\rangle)
\\|10\rangle
&\longmapsto
|\psi_{10}\rangle \coloneqq \frac{1}{\sqrt{2}}(|00\rangle-|11\rangle)
\\|11\rangle
&\longmapsto
|\psi_{11}\rangle \coloneqq \frac{1}{\sqrt{2}}(|01\rangle-|10\rangle)
\end{aligned}
The more standard notation for these states, however, is the following:
\begin{aligned}
\Phi^+ &\coloneqq |\psi_{00}\rangle
\\\Psi^+ &\coloneqq |\psi_{01}\rangle
\\\Phi^- &\coloneqq |\psi_{10}\rangle
\\\Psi^-&\coloneqq |\psi_{11}\rangle
\end{aligned}
(and this is the notation that we will use from now on).
The Bell states form an orthonormal basis in the Hilbert space \mathcal{H}_1\otimes\mathcal{H}_2 of two qubits.
We can perform measurements in the Bell basis: the easiest way to do it in practice is to “rotate” the Bell basis to the standard basis, and then perform the measurement in the standard basis.
Indeed, if we reverse the circuit (running it from right to left), then we get a circuit which maps the Bell state |\psi_{ij}\rangle to the corresponding state |ij\rangle in the standard basis.
This unitary mapping allows us to “implement” the projections on Bell states by applying the reversed circuit followed by the usual qubit-by-qubit measurement in the standard basis.
The Bell states are said to be maximally entangled, since their reduced density operators are maximally mixed (a notion that we will define in Section 8.3).
Roughly, this means that the outcomes of any measurement performed on them are completely random.
This property — having maximal entropy (in some sense) — makes the Bell states incredibly useful for many applications, and we shall see some of them now.