Pauli normalisers
There are two subgroups that pop up once we choose a stabiliser \mathcal{S}.
The subgroup of \mathcal{P}_n consisting of all elements that commute which every element of \mathcal{S} is called the centraliser of \mathcal{S}, denoted by
Z(\mathcal{S}) = \{g\in\mathcal{P}_n \mid gsg^{-1}=s\text{ for all }s\in\mathcal{S}\}
and the other is the one that we have already seen: the normaliser
N(\mathcal{S}) = \{g\in\mathcal{P}_n \mid gsg^{-1}\in\mathcal{S}\text{ for all }s\in\mathcal{S}\}.
These two are, in general, distinct but related: for the normaliser we ask that gsg^{-1}=s' for some arbitrary s'\in\mathcal{S}, and for the centraliser we additionally ask that s'=s.
However, in the case of Pauli groups, these two subgroups coincide, because gsg^{-1}=s' if and only if sg=gs', but since any two elements of the Pauli group either commute or anticommute, this implies that s'=s or s'=-s; but we have already seen (and proven, in Exercise 7.8.4) that if s is in a stabiliser then -s cannot be, and so it must be the case that s'=s.
In summary, given a stabiliser, we get a corresponding normaliser, and given the normaliser (which, in our case, is the same thing as the centraliser), we get two interesting quotient groups to study.
By the definition of the normaliser, \mathcal{S} is normal in N(\mathcal{S}).
What is less obvious is that N(S) itself is normal in \mathcal{P}_n.
To prove this, let g\in\mathcal{P}_n and consider gng^{-1}, for some n\in N(\mathcal{S}).
We need to show that gng^{-1}\in N(S).
For any s\in\mathcal{S},
(gng^{-1})s = s(gng^{-1})
because either s commutes with both g and g^{-1}, or it anticommutes with both g and g^{-1}, in which case the two minus signs cancel out.
Either way, s commutes with gng^{-1}, and so, by definition, gng^{-1}\in N(\mathcal{S}).
So \mathcal{S} in normal in N(\mathcal{S}) by definition, and N(\mathcal{S}) is normal in \mathcal{P}_n by the above; but recall that this does not imply that \mathcal{S} is normal in \mathcal{P}_n.
Indeed, pick any element g\in\mathcal{P}_n that anticommutes with some s\in\mathcal{S}, so that gsg^{-1}=-s; but we already know that if s\in\mathcal{S} then -s\not\in\mathcal{S}.
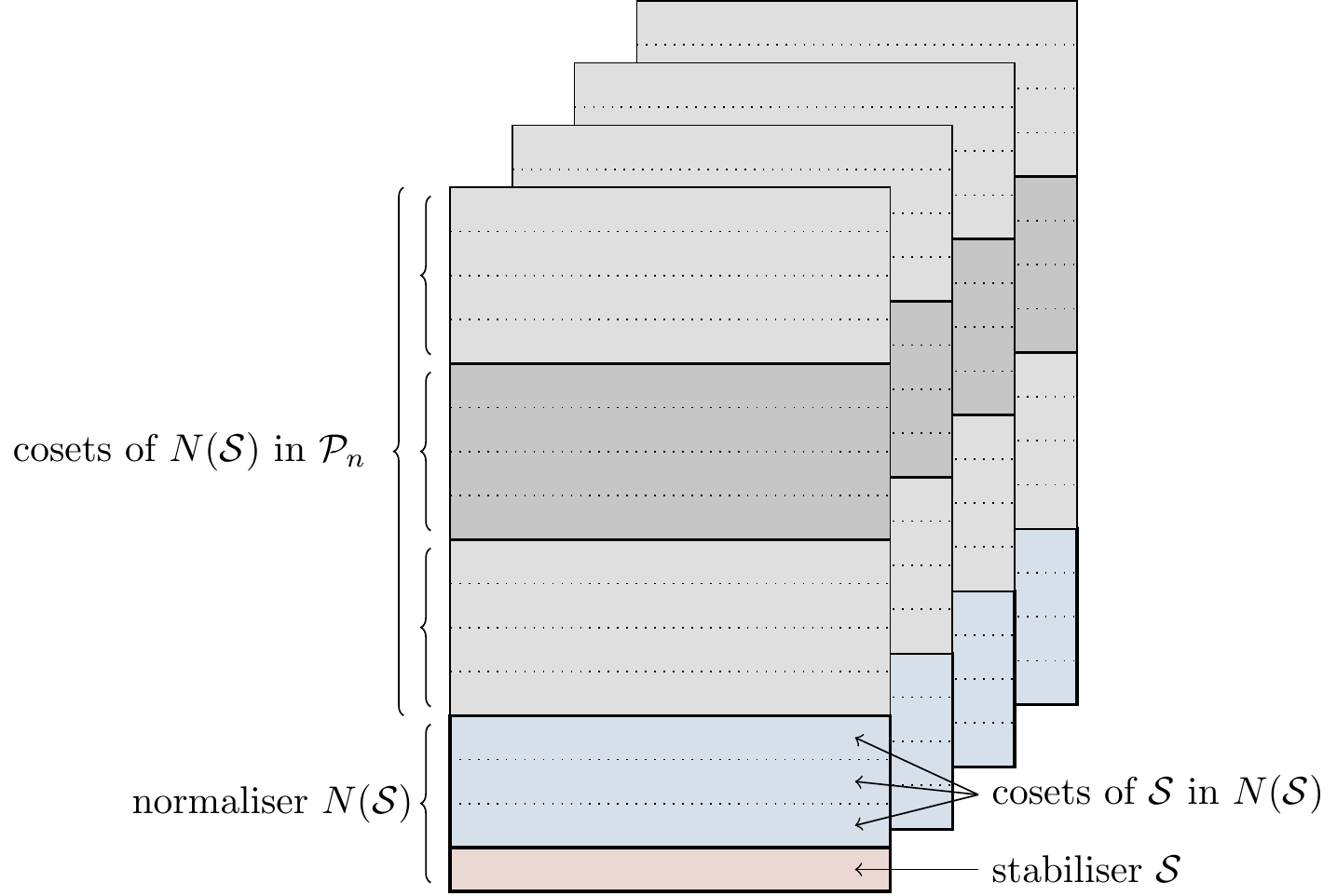
With these normal subgroups \mathcal{S}\triangleleft N(\mathcal{S})\triangleleft\mathcal{P}_n we can form two quotient groups, arranging things into cosets: N(\mathcal{S})/\mathcal{S} and \mathcal{P}_n/N(\mathcal{S}).
This is visualised in Figure 7.2.
Note that we can also form cosets of \mathcal{S} in \mathcal{P}_n, but since this is not a normal subgroup the left cosets will be different from the right cosets, and we cannot construct a quotient group \mathcal{P}_n/\mathcal{S}.
This resulting structure — any Pauli stabiliser slicing its normaliser into cosets, and this normaliser in turn slicing the Pauli group into cosets — will be very useful when we discuss quantum error correction and fault tolerance in Sections 13 and 14, and we can explain a bit how this will work now.
The stabiliser will partition the Hilbert space of n qubits into subspaces, and the one that is fixed by the stabiliser will be chosen as a codespace.
All operators in the normaliser will then become logical operators on the codespace, and the cosets of the normaliser in \mathcal{P}_n will group together operators that describe errors of a similar type (those with the same error syndrome).
It will be a useful fact to know that \mathcal{P}_n/N(\mathcal{S}) is abelian — we show this in Exercise 7.8.6.
Finally, let’s count some elements.
We have already seen that |\mathcal{P}_n|=4\cdot 4^n=4^{n+1}, and that if \mathcal{S} has r generators then |\mathcal{S}|=2^r.
But what about N(\mathcal{S})?
By definition, the normaliser consists of all the operators that commute with all the generators of the stabiliser.
There are 4\cdot(4^n/2) that commute with the first generator, half of which also commute with the second generator, a further half of which also commute with the third generator, and so on.
So we have that |N(\mathcal{S})|=4\cdot(4^n/2^r).
Finally we have the two quotient groups: N(\mathcal{S})/\mathcal{S} has 4\cdot(4^n/4^r)=4^{n-r+1} elements and is isomorphic to \mathcal{P}_{n-r}; and \mathcal{P}_n/N(\mathcal{S}) has (4\cdot4^n)/(4\cdot(4^n/2^r))=2^r elements.