13.10 Correcting any single error: Shor [[9,1,3]]

In Section 13.9 we derived the encoding circuit for the Shor [[9,1,3]] code, so now let’s go from the top and put all the pieces together to understand how this gives an error correction procedure for all possible single-qubit errors.273

To start, we encode our qubit with the phase-flip code \begin{aligned} |0\rangle &\longmapsto |+\rangle|+\rangle|+\rangle \\|1\rangle &\longmapsto |-\rangle|-\rangle|-\rangle \end{aligned} and then we encode each of the resulting three qubits with the bit-flip code \begin{aligned} |0\rangle &\longmapsto |0\rangle|0\rangle|0\rangle \\|1\rangle &\longmapsto |1\rangle|1\rangle|1\rangle \end{aligned} resulting in a net effect of \begin{aligned} |0\rangle &\longmapsto (|000\rangle+|111\rangle)(|000\rangle+|111\rangle)(|000\rangle+|111\rangle)/\sqrt{8} \\|1\rangle &\longmapsto (|000\rangle-|111\rangle)(|000\rangle-|111\rangle)(|000\rangle-|111\rangle)/\sqrt{8}. \end{aligned} \tag{$\ddagger$}

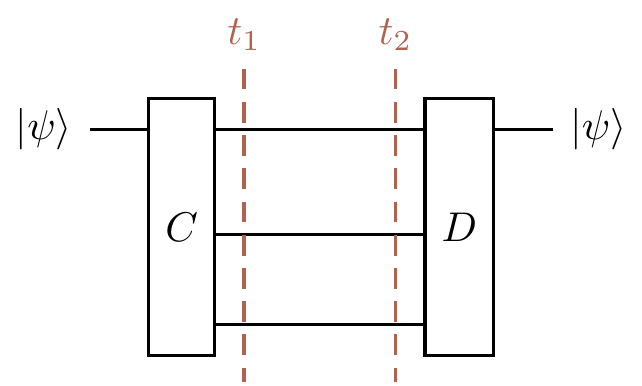
In order to understand how this code works, it is helpful to look at the complete circuit diagram, so let’s build it up in a compositional way. Rather than drawing the entire circuits from Sections 13.7 and 13.8 again, let’s simply draw them as consisting of an encoding gate C and a decoding gate D, separated by a zone [t_1,t_2] that corresponds to transmission over the noisy channel. Then the bit-flip correction circuit looks like

and the phase-flip correction looks the same, but with Hadamard gates sandwiching the transmission zone, so

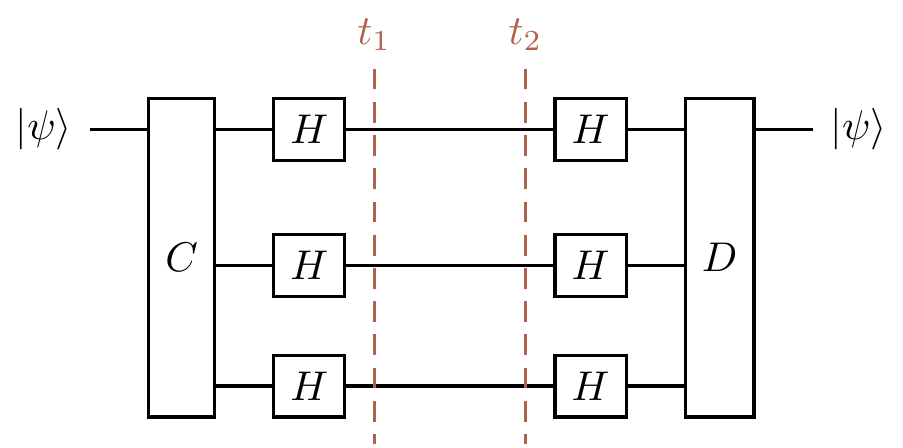
Then we can nest the bit-flip correction circuit into the phase-flip correction circuit by inserting a copy on each of the three wires in the transmission zone, giving us the circuit that implements the encoding of Equation (\ddagger), as shown in Figure 13.10.

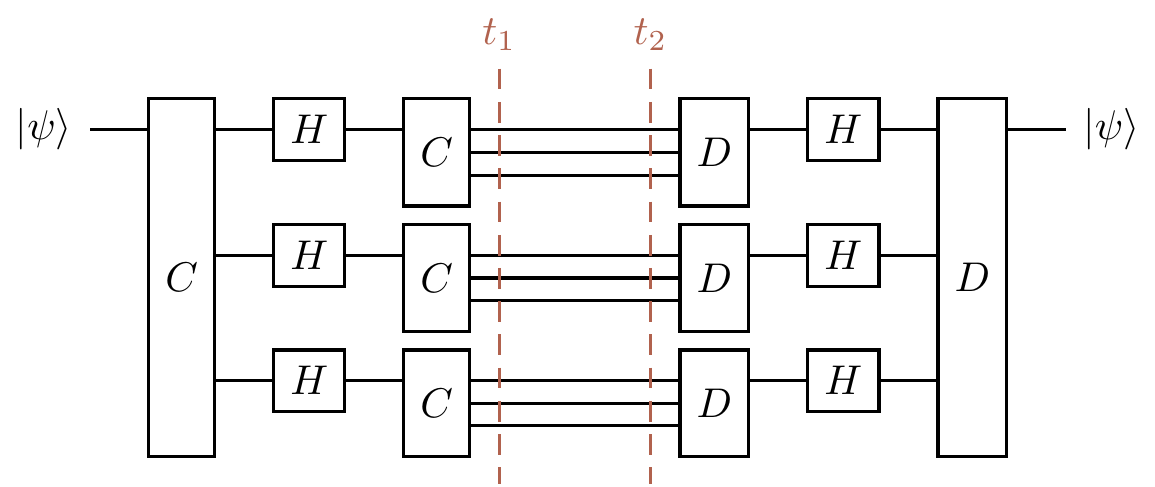
Nesting the two correction circuits: one copy of the bit-flip correction circuit on each wire of the phase-flip correction circuit.

Figure 13.10: Nesting the two correction circuits: one copy of the bit-flip correction circuit on each wire of the phase-flip correction circuit.

We have already seen the idea of sequential composition compared to parallel composition, when we talk about the difference between matrix multiplication BA (“do A then B”) and the tensor product A\otimes B (“do A to one part and B to the other”). Neither type of composition can deal with choices: if A and B are of the right size, then BA (or A\otimes B) is either defined or it isn’t. However, there are some subtleties to be aware of.

For example, associativity of a composition operation tells us that we can forget about brackets if we just have the same type of composition over and over, since (CB)A=C(BA). It seems like every operation we ever meet is associative (indeed, it’s even baked into the definition of what it means to be a group), but it turns out that non-associative operations are just as interesting as non-commutative ones. But the story doesn’t stop there! What if we want to study “the next thing up” from associativity, whatever this might be? Or what if we want to study operations that have more than two inputs, and maybe even more than one output? Trying to answer questions like this leads us to operads and their algebras.

Looking again at Figure 13.10, we see that we could have composed the bit-flip correction circuits in a different way, placing them one after the other, but we instead wanted to nest them. All that matters in order for us to be able to do either one of these compositions (whether or not we can find any use for it!) is that the number of input and output wires match up. Working with (algebras over) operads has a similar flavour, and you will find yourself drawing lots of little diagrams and then either putting them side-by-side or nesting copies of one inside bits of the other in various different ways. You might find some intriguing pictures if you search for the little cubes operad, or the Swiss cheese operad. One particularly nice introduction is Tai-Danae Bradley’s “What is an Operad?”.

Now, if an X error occurs on one of the nine qubits in the circuit in Figure 13.10 during the time interval [t_1,t_2], it will be corrected by the corresponding inner three-qubit repetition code that corrects for bit-flips. In fact, this scheme can tolerate up to three bit-flip errors provided that they occur in different blocks.274 For example, writing X_i to mean an X error on the i-th qubit, if X_1, X_5, and X_7 all occur then they will all be corrected, but if X_1 and X_2 both occur then the resulting error will not be corrected.

Next, if a Z error occurs on one of the qubits, say the first one, we know that it will not be corrected by the inner encoding–decoding circuit (the one taking place on the top three qubits), but it will be passed along and then corrected “one level up”, by the outer encoding–decoding circuit (the one taking place on the first, fourth, and seventh qubits).

Finally, what about if a Y error occurs? Well, since Y=ZX, the inner circuit will correct the X part of the error, and the outer circuit will correct the Z part275

So quantum error correction is indeed possible: we can remove the unwanted effects of decoherence during transmission through a channel. However, this process of encode–transmit–decode doesn’t really cover the practical scenario of computation, since in reality we are constantly trying to process our data, and noise could enter at any moment. One thus has to compute on the encoded states the whole time, whilst also somehow ensuring that even faults occurring during an error correction cycle don’t adversely affect the computation. This is known as fault tolerance, and studying this, using the stabiliser formalisation of Chapter 7, is the goal of Chapter 14.

  1. Although nine qubits is actually more than necessary (we can achieve the same result with a different scheme that only uses five), this code, proposed by Shor in 1995, allows us to more easily see what’s really going on.↩︎

  2. We will explain why this condition of “occurring in different blocks” is necessary in Section 14.7.↩︎

  3. As per usual, any resulting global phase doesn’t matter.↩︎