14.11 Remarks and exercises

14.11.1 Error correcting conditions for the three-qubit code

When building the Shor [[9,1,3]] code, we used the three-qubit code twice: once to correct for X-errors, and once for Z-errors. However, there is no reason why we couldn’t instead have used one copy to correct for Y-errors instead of X-errors, and we can see this using the dot-error diagrams.

Consider the stabiliser code given by \mathcal{S}=\langle ZZ\mathbf{1},\mathbf{1}ZZ\rangle. In Figure 14.13 we draw all the computational errors of weight at most 1, and we see that this does not describe a correctable scenario. That is, as we already know, the three-qubit code cannot alone correct for all single-qubit errors.

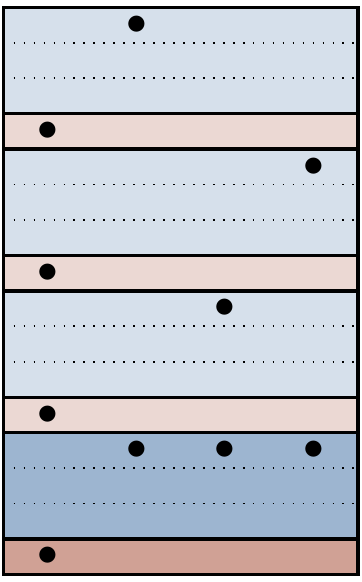
Figure 14.13: All computational errors of weight at most 1 for the three-qubit code given by \langle ZZ\mathbf{1},\mathbf{1}ZZ\rangle. Note that this describes a non-correctable scenario. In fact, both of the two rules are broken.

But now let’s look at X-, Y-, and Z-errors all individually and see what happens. As Figure 14.14 shows, the three-qubit code given by \langle ZZ\mathbf{1},\mathbf{1}ZZ\rangle can correct for all X-errors (as we already knew), but also for all Y-errors!

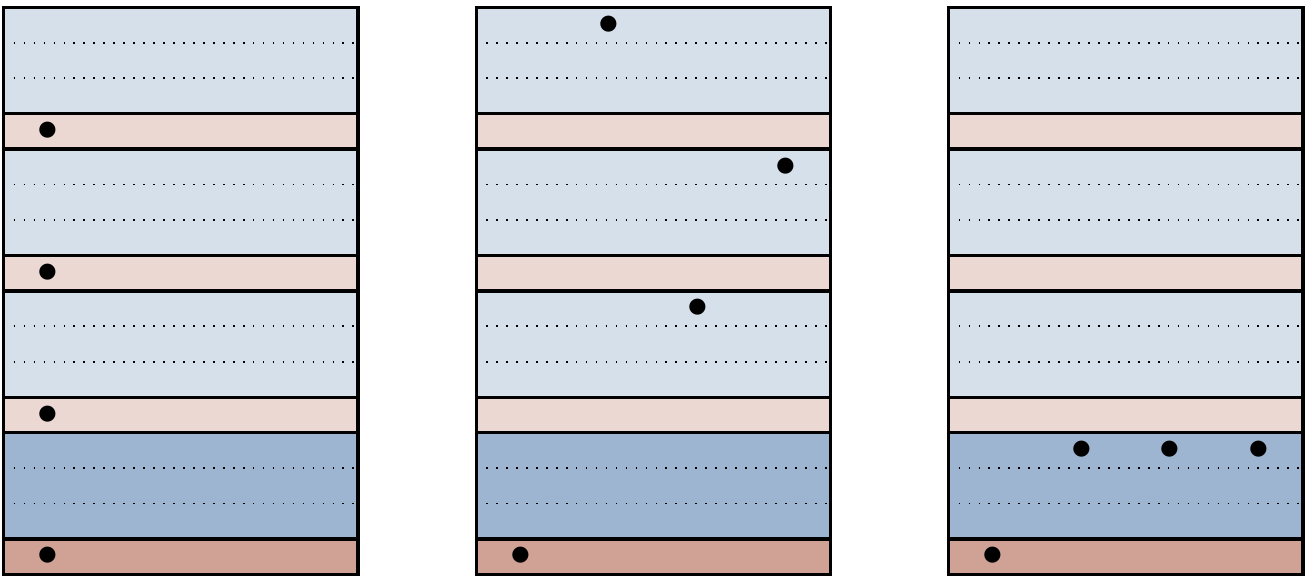
Figure 14.14: Different types of computational errors of weight at most 1. Left to right: X-type errors (correctable); Y-type errors (correctable); Z-type errors (non-correctable).

14.11.2 The smallest d=3 code, full stop

We have already seen the Shor [[9,1,3]] code, which can protect against any single-qubit error. Despite its simplicity, it is not the smallest code that can do this: that title belongs to the [[5,1,3]] stabiliser code, given by \mathcal{S} = \langle XZZX\mathbf{1}, \mathbf{1}ZXXZ, X\mathbf{1}XZZ, ZX\mathbf{1}XZ\rangle shown as a Tanner graph in Figure ??. Note that the stabiliser generators (i.e. parity checks) are related to each other by cyclic shifts: we just take different length-five chunks from the infinite string XZZX\mathbf{1}XZZX\mathbf{1}XZZX\mathbf{1}\ldots. This code is unusual compared to the ones we have seen before, since it’s actually impossible to write its generators as operators that consist of either all X or all Z.

Figure 14.15: The Tanner graph for the [[5,1,3]] stabiliser code. Solid lines represent X-checks, and dashed ones Z-checks.

This [[5,1,3]] code truly is optimal, in that it is the smallest possible³²¹ quantum error correcting code with d=3. Indeed, suppose that we have n qubits representing one logical qubit, and each error X, Y, or Z on any of these n qubits maps the two-dimensional codespace to a different, mutually orthogonal subspace.³²² This means that we have to fit the codespace, plus 3n two-dimensional subspaces, into the 2^n-dimensional Hilbert space associated with the n qubits. This implies that we need to satisfy 2(1+3n) \leqslant 2^n which tells us that we must have at least n\geqslant 5.

The counting argument above tells us that the smallest code must have at least five qubits, but doesn’t tell us if we can actually make one with exactly five qubits! How do we actually go about finding optimal codes then? The answer is simply that we do not know — there is no universal prescription for designing optimal quantum codes. But we do know quite a few things about designing good quantum codes.

One last thing to mention is how this code displays that quantum codes can be used for more than just error correction. The [[5,1,3]] code gives a way of designing a ((3,5)) quantum secret sharing protocol.

14.11.3 Hamming code encodings and decodings

1. How is the binary message 0101 encoded in the Hamming [7,4,3] code?
2. If we receive the string 1011011 from Alice, who encoded her message in the Hamming [7,4,3] code, then what is the error syndrome? What correction should we make? What is the decoded message?

14.11.4 Generator and parity-check matrices

Show that, if the (n\times k) generator matrix for an [n,k,d] linear code is written in the form G = \begin{bmatrix} \mathbf{1} \\P \end{bmatrix} where P is an ((n-k)\times k) binary matrix, then the parity-check matrix can be written as H = \begin{bmatrix} P & \mathbf{1} \end{bmatrix}.

14.11.5 A big parity check matrix

Consider the following parity-check matrix of a classical [n,k,7] code: \left[ \begin{array}{cccccccccccccccccccccccc} 1&0&0&1&1&1&0&0&0&1&1&1&1&0&0&0&0&0&0&0&0&0&0 \\1&0&1&0&1&1&0&1&1&0&0&1&0&1&0&0&0&0&0&0&0&0&0 \\1&0&1&1&0&1&1&0&1&0&0&0&0&0&1&0&0&0&0&0&0&0&0 \\1&0&1&1&1&0&1&1&0&1&0&0&0&0&0&1&0&0&0&0&0&0&0 \\1&1&0&0&1&1&1&0&1&1&0&0&0&0&0&0&1&0&0&0&0&0&0 \\1&1&0&1&0&1&1&1&0&0&0&1&0&0&0&0&0&1&0&0&0&0&0 \\1&1&0&1&1&0&0&1&1&0&1&0&0&0&0&0&0&0&1&0&0&0&0 \\1&1&1&0&0&1&0&1&0&1&1&0&0&0&0&0&0&0&0&1&0&0&0 \\1&1&1&0&1&0&1&0&0&0&1&1&0&0&0&0&0&0&0&0&1&0&0 \\1&1&1&1&0&0&0&0&1&1&0&1&0&0&0&0&0&0&0&0&0&1&0 \\0&1&1&1&1&1&1&1&1&1&1&1&0&0&0&0&0&0&0&0&0&0&1 \end{array} \right]

1. What are the values of the parameters n and k?

2. If we receive the bit string x = 00101001011011000110101 and assume that no more than three errors have occurred, what are the locations of the errors?

3. Show that we could use two copies of this code to build a CSS code.

4. If we build a CSS code using this classical code, what parameters does it have? That is, what is its specification as an [[n,k,d]] code?

5. Given a state |\psi\rangle of 23 qubits, how would you measure the value of the first stabiliser X_1X_4X_5X_6X_{10}X_{11}X_{12}X_{13}?

6. If we were to write out |0\rangle_L for the CSS code, how many different basis states would be in the superposition?

14.11.6 Using Tanner graphs

Consider the Tanner graph below.

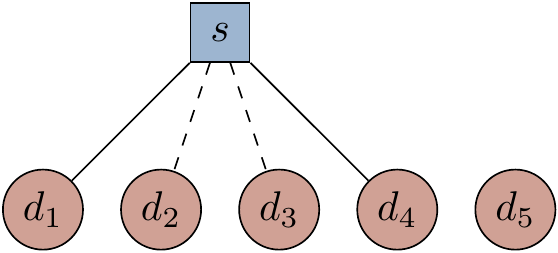
Recall that we use solid lines to denote X-parity checks and dashed lines to denote Z-parity checks.

1. What stabiliser does this Tanner graph define?
2. Add to the Tanner graph the definition for a second stabiliser g_2=\mathbf{1}XZZX. How can we visually confirm that the two stabilisers commute?

At the end of Section 14.1, in Figure 14.3, we claimed an equivalence between Tanner graphs (for detecting the parity of X errors) and circuits. Consider the simpler example below.

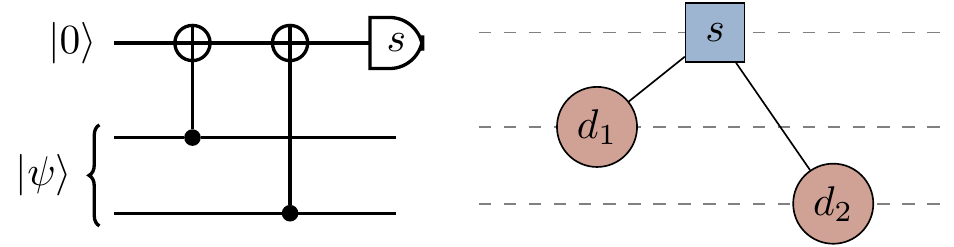
3. Draw the circuit³²³ for measuring the parity of Z-errors.
4. Draw the Tanner graph for the Shor [[9,1,3]] code.

14.11.7 Five-qubit repetition code

Consider the five-qubit repetition code \begin{aligned} |0\rangle &\mapsto |+\rangle^{\otimes5} \\|1\rangle &\mapsto |-\rangle^{\otimes5}. \end{aligned}

1. What are the stabilisers of this code?
2. What is the normaliser of this code?
3. Which of the following sets of errors satisfy the error correcting conditions for this code? (Recall that the identity \mathbf{1} is always implicitly assumed to be inside the set of errors).
   1. \{X_1, Z_5\}
   2. \{X_1, X_2, X_3, X_4\}
   3. \{Z_1, Z_2, Z_3, Z_4\}
   4. \{Z_1Z_2, Z_2Z_4, Z_1Z_4\}

14.11.8 An error in the Steane [[7,1,3]] code

One logical qubit is encoded in seven physical qubits using the Steane [[7,1,3]] code, which then experiences the error E = X\mathbf{1}Y\mathbf{1}\mathbf{1}Z\mathbf{1}.

1. What is the resulting error syndrome?
2. What is the smallest-weight error with the same error syndrome as E?
3. If we apply the smallest-weight error from above as our correction, then what is the net logical error on the encoded qubit?

14.11.9 Non-degenerate codes

An [n,k,d] code is said to be non-degenerate if every Pauli operator of weight \leqslant\lfloor d/2\rfloor has a distinct error syndrome.

Prove that all the stabilisers for a non-degenerate code have weight \geqslant d.

14.11.10 The smallest d=3 CSS code

The [[7,1,3]] code is the smallest possible CSS code with distance d=3. Let’s prove that now, making the simplification that we will only consider non-degenerate codes.

1. If we construct a CSS code using two parity-check matrices H_1 and H_2, with m_1 and m_2 rows (respectively), and we want our code to encode one logical qubit into n physical qubits, then how are the numbers m_1, m_2, and n related?

2. Explain why the columns of a non-degenerate d=3 code must be distinct. Hence conclude that 2^{m_i}\geqslant n+1 for i=1,2.

3. Conclude that the smallest possible non-degenerate CSS code with d=3 has n=7 qubits.

14.11.11 CSS codes from a single matrix

Let H be an (n\times m) binary matrix, with m>n, whose rows are linearly independent. When taken as a parity-check matrix, it thus defines an [m,m-n,d] code. Even though H^T cannot be the parity-check matrix of a code (simply because m>n), it still has a well defined distance d^T.

Show that \begin{aligned} H_X &= \begin{bmatrix} \mathbf{1}_{m\times m}\otimes H & H^T\otimes\mathbf{1}_{n\times n} \end{bmatrix} \\H_Z &= \begin{bmatrix} H\otimes\mathbf{1}_{n\times n} & \mathbf{1}_{m\times m}\otimes H^T \end{bmatrix} \end{aligned} defines a CSS code with specification [[n^2+m^2,(n-m)^2,\min(d,d^t)]].

14.11.12 Error-correcting conditions, algebraically

Let \mathcal{S}\leqslant\mathcal{P}_n be a stabiliser group, and let \mathcal{E}\subseteq\mathcal{P}_n be a set such that \mathbf{1}\in\mathcal{E}. Prove that the stabiliser code defined by \mathcal{S} can perfectly correct for all errors in \mathcal{E} if and only if E_1^\dagger E_2 \not\in N(\mathcal{S})\setminus\mathcal{S} for all E_1,E_2\in\mathcal{E}.

14.11.13 Steane error correction: towards fault tolerance

We have seen how we can measure the stabilisers of a stabiliser code by using a Hadamard test, resulting in \pm1 outcomes. From these, we can determine where the errors are likely to have occurred and then correct them. In Chapter 15, we will see that the scenario of fault-tolerant computation requires us to be very careful with how we construct our error-correcting circuits in order to minimise the propagation of faults that occur during the error-process itself. A particularly useful strategy is to not have multiple qubits interacting, but this contradicts the measurements of the stabilisers, since these, by definition, act on many qubits. There are a variety of ways to deal with this. In the case of CSS codes, Steane himself provided a particularly elegant method, which we will now explore.

Note that, while we are motivated by the possibility of there being faults during the error correction, for now we will still assume that the error-correction process proceeds perfectly, and we are only trying to identify and fix errors on the incoming (logical) state |\psi\rangle_L.

As we shall later see, CSS codes all have transversal \texttt{c-NOT} gates: applying a \texttt{c-NOT} to each physical qubit gives exactly the effect of a \texttt{c-NOT} on the logical qubit. In other words, we can implement the logical operator \texttt{c-NOT}_L by taking a tensor product of usual controlled-\texttt{NOT} gates. What this means for us right now is that, at the logical level, we can consider circuits such as³²⁴

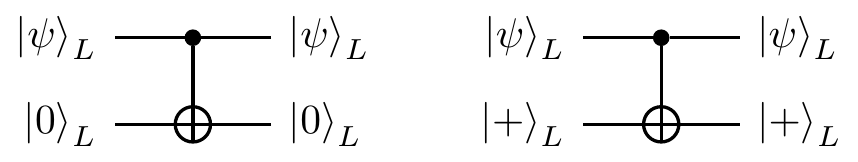
1. Verify that the above circuits do indeed have the claimed outputs.

This means that, if the qubits are in the logical space (i.e. have undergone no errors), then the action of the circuit is trivial. So what happens if there’s an error? Let’s assume that we’re working with an [[n,1,d]] CSS code.

2. If an X or Z error has already affected the input logical state |\psi\rangle_L on a specific physical qubit (say, the i-th) in the circuit on the left above, what are the possible errors on the final state?
3. If an X or Z error has already affected the input logical state |\psi\rangle_L on a specific physical qubit (say, the i-th) in the circuit on the right above, what are the possible errors on the final state?

In other words, we see that single errors cannot propagate to more than one error on each logical qubit. This will prove to be very useful when thinking about fault tolerance, as the same is also true if errors occur during the circuit. Now we should see how error correction works. Let’s consider the circuit on the left above.

4. The X stabilisers are defined by the rows of a parity-check matrix H. We measure each physical qubit of the second logical qubit, |0\rangle_L, in the X basis at the end of the circuit. In the absence of any errors, we get a measurement outcome y\in\{0,1\}^n. What is the value of H\cdot y?
5. If a weight-w Z-error occurs on the state |\psi\rangle_L before the (transversal) controlled-\texttt{NOT}, where 2w<d, then what are the possible measurement outcomes? How do we identify which corrections to make?

So this circuit allows us to correct Z-errors on the input, but it does absolutely nothing to X-errors.

6. Show that the circuit on the right above enables the correction of X-errors in a similar way, where the extra logical qubit is now measured by measuring each individual qubit in the Z (i.e. computational) basis.

---

321. Note that this code is not a CSS code! To prove this, we could use theorems about transversal gates. The smallest CSS code with d=3 is described in Exercise 14.11.10.↩︎

322. Here we are tacitly assuming that the code is non-degenerate (see Exercise 14.11.9).↩︎

323. Hint: you know what the circuit for X-parity checks looks like, so do the standard thing and swap every X for Z (and vice versa), transform anything in the Z-basis to the X-basis (and vice versa), and then check if the resulting circuit can be simplified by cancelling out any gates; don’t forget that a \texttt{c-NOT} is secretly a \texttt{c-}X!↩︎

324. We are assuming the availability of the logical states |0\rangle_L and |+\rangle_L, but state preparation is another challenge that we will eventually have to deal with!↩︎