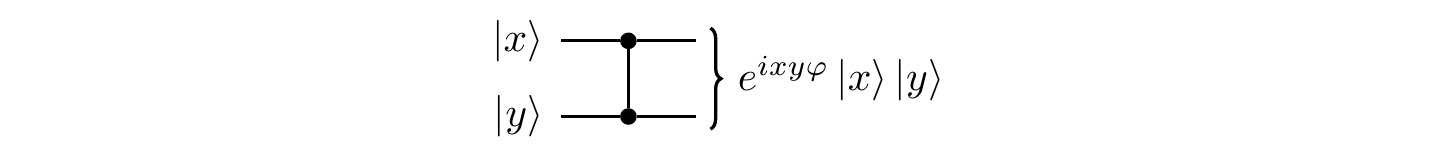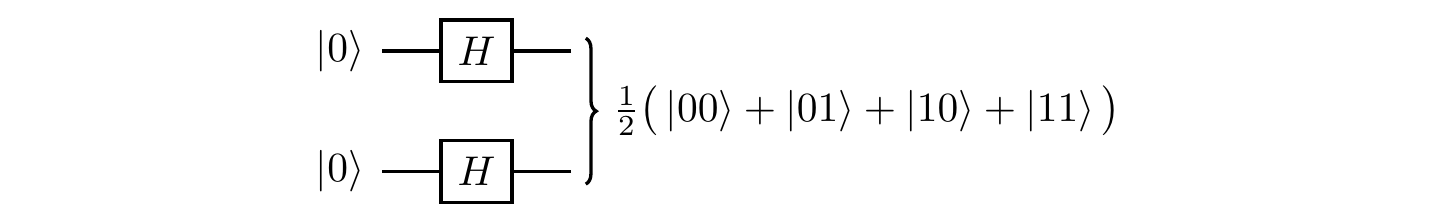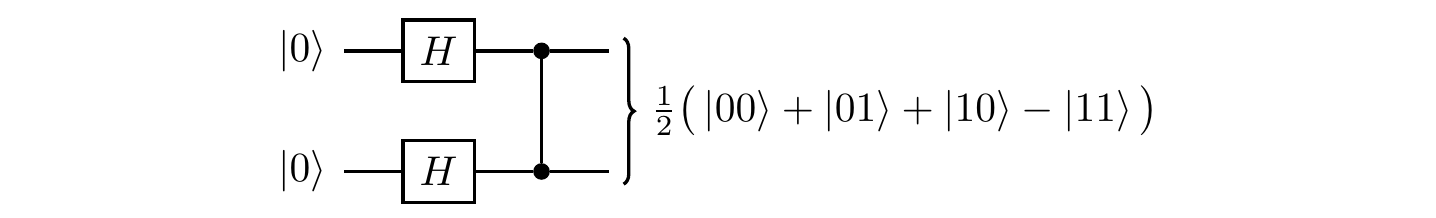Controlled-phase and controlled-U
Needless to say, not everything is about the controlled-\texttt{NOT} gate.
Another common two-qubit gate is the controlled-phase gate, denoted \texttt{c-}P_\varphi.
| Controlled-phase |
\left[\begin{array}{c|c}\begin{matrix}1&0\\0&1\end{matrix}&\begin{matrix}0&0\\0&0\end{matrix}\\\hline\begin{matrix}0&0\\0&0\end{matrix}&\begin{matrix}1&0\\0&e^{i\varphi}\end{matrix}\end{array}\right] |
We can also represent the \texttt{c-}P_\varphi gate using the circuit notation, as in Figure 5.2.
Again, the matrix is written in the computational basis \{|00\rangle,|01\rangle,|10\rangle,|11\rangle\}.
If we do not specify the phase then we usually assume that \varphi=\pi, in which case we call this operation the controlled-Z gate, which acts as |0\rangle\langle 0|\otimes\mathbf{1}+ |1\rangle\langle 1|\otimes Z.
Here Z refers again to the Pauli phase-flip \sigma_z\equiv Z operation.
In order to see the entangling power of the controlled-phase shift gate, consider the following circuit.
(Generating entanglement, again).

In this circuit, first the two Hadamard gates prepare the equally-weighted superposition of all states from the computational basis
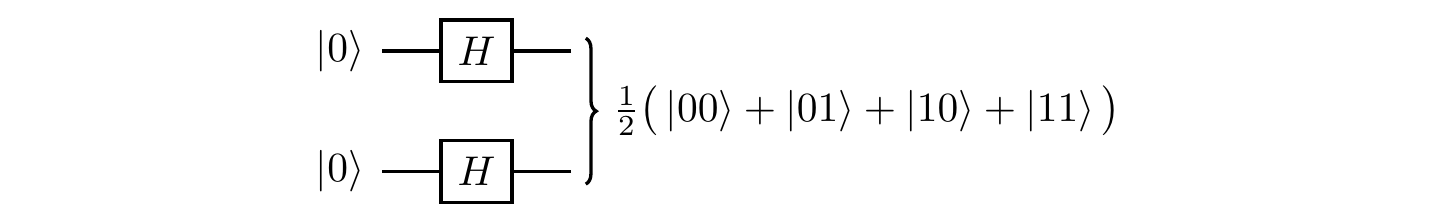
and then the controlled-Z operation flips the sign in front of |11\rangle
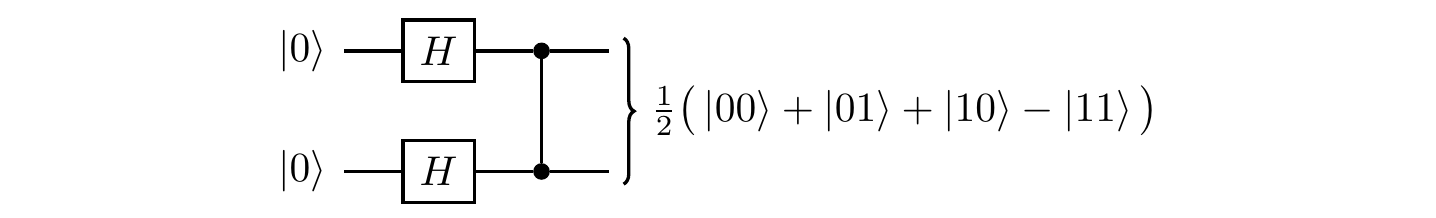
which results in an entangled state.
In fact, both \texttt{c-NOT} and \texttt{c-}P_\varphi are specific examples of the more general construction of a controlled-U gate:
\texttt{c-}U
= |0\rangle\langle 0|\otimes\mathbf{1}+ |1\rangle\langle 1|\otimes U
where U is an arbitrary single-qubit unitary transformation U.
| Controlled-U |
\left[\begin{array}{c|c}\begin{matrix}1&0\\0&1\end{matrix}&\begin{matrix}0&0\\0&0\end{matrix}\\\hline\begin{matrix}0&0\\0&0\end{matrix}&U\end{array}\right] |
We can also represent the \texttt{c-}U gate using the circuit notation, as in Figure 5.3.
We can go even further and consider a more general unitary operation: the two-qubit x-controlled-U gate:
\sum_x |x\rangle\langle x|\otimes U_x
\equiv
|0\rangle\langle 0|\otimes U_0 + |1\rangle\langle 1|\otimes U_1
where each U_x is a unitary transformation that is applied to the second qubit only if the first one is in state |x\rangle.
In general, an x-controlled-U gate can be defined on two registers of arbitrary size n and m, with x\in\{0,1\}^n and the U_x being (2^m\times 2^m) unitary matrices acting on the second register.