6.4 Bell’s theorem via CHSH

Continuing this story of Alice and Bob with their observables and pairs of qubits, let us first rephrase things in the formalism of quantum mechanics that we’ve been building up. The observables A_1, A_2, B_1, B_2 become (2\times 2) Hermitian matrices, each with the two eigenvalues \pm 1, and \langle S\rangle becomes the expected value of the (4\times 4) CHSH matrix S = A_1\otimes(B_1-B_2) + A_2\otimes(B_1+B_2). We can now evaluate \langle S\rangle using quantum theory.

Actually performing these measurements described by S on a pair of qubits is known as a CHSH test, or Bell test.

If the two qubits are in the singlet state |\psi\rangle = \frac{1}{\sqrt{2}} \left( |01\rangle-|10\rangle \right) then we have already seen (Section 6.2) that \langle A\otimes B\rangle = -\vec{a}\cdot\vec{b}. So if we choose vectors \vec{a}_1, \vec{a}_2, \vec{b}_1, and \vec{b}_2 as shown in Figure 6.1, then the corresponding matrices131 satisfy \begin{aligned} \langle A_1\otimes B_1\rangle &= \langle A_2\otimes B_1\rangle = \langle A_2\otimes B_2\rangle = \frac{1}{\sqrt{2}} \\\langle A_1\otimes B_2\rangle &= -\frac{1}{\sqrt{2}}. \end{aligned}

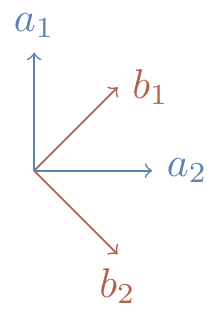
The relative angle between the two perpendicular pairs is 45^\circ.

Figure 6.1: The relative angle between the two perpendicular pairs is 45^\circ.

Plugging these values in, we get that \langle A_1 B_1\rangle - \langle A_1 B_2\rangle + \langle A_2 B_1\rangle + \langle A_2 B_2\rangle = -2\sqrt{2}, which obviously violates CHSH inequality: -2\sqrt{2} is strictly less than -2!

But here is the really important part of this discussion: this violation of the CHSH has been observed in a number of painstakingly careful experiments — this is not just theoretical! The early efforts in these experiments were truly heroic, with many many layers of complexity; today, however, such experiments are routine.

Bell’s theorem. The behaviour of entangled quantum systems cannot be explained by local hidden variables. In other words, outcomes in quantum mechanics really are random, and it’s not simply our lack of knowledge about some background process.

If we can enforce locality in an experimental setup (for example, by ensuring that Alice and Bob are sufficiently far apart so that there is not enough time between Alice making a measurement and Bob receiving his measurement result) then an experimental verification of the CHSH test proves to us that the system is behaving in an inherently non-classical and, importantly, unpredictable manner. This means that this is a good test to see if our devices are performing as they are supposed to, and are untampered by any potential eavesdroppers.132 In other words, the CHSH test is key for securing quantum protocols, as we will explain in Section 6.6.

  1. That is, A_1=\vec{a}_1\cdot\vec{\sigma}, and so on.↩︎

  2. If an eavesdropper has observed our system to the extent that they can predict out outcomes, then that very predictability means that there is a hidden-variable description of the system, and the CHSH inequality is not violated.↩︎