Phase estimation
In Section 10.4, we took the problem of binary observable measurement and at Deutsch’s algorithm, which uses quantum Boolean function evaluation as the controlled-U gate.
Now we’re going to generalise the binary observable measurement problem to other controlled-U gates, trying to deduce the value of an unknown phase that can be a lot more general than simply 0 or \pi. Afterwards, we’ll explain how this is the first step towards Shor’s algorithm for prime factorisation.
Let’s start by rephrasing the binary observable measurement problem in terms of phase estimation (or eigenvalue estimation).
Recall the problem: we are handed some phase gate of unknown phase \varphi, but we are promised that \varphi is either 0 or \pi; we want to figure out which one it is by running a simple circuit one time.
But this is entirely equivalent to having access to an oracle that computes a controlled-U gate, along with having an eigenstate |u\rangle with eigenvalue \pm1 (i.e. e^{i\varphi} for \varphi\in\{0,\pi\}), since this acts as a phase gate of phase 0 or \pi (depending on whether the eigenvalue is +1 or -1) on the first register when we plug in |u\rangle to the second register.
This is just phase kick-back again!
So let’s state the problem this way, and use the solution that we have already described in Section 10.4 (which is really the circuit that we saw all the way back in Section 5.12).
(Binary phase estimation).
We are presented with an oracle that computes a controlled-U gate, along with an eigenstate |u\rangle of U with eigenvalue e^{i\varphi}
We are promised that \varphi is either 0 or \pi.
Our task is to determine, using the fewest queries possible, the value of \varphi.
(Controlled-U interference).
First register: 1 qubit. Second register: 1 qubit.

So we see that the eigenvalues being \pm1, or, equivalently, \varphi being 0 or \pi, is fundamental to this story — this is what we want to generalise, so that we can deal with more values of \varphi.
We are presented with an oracle that computes a controlled-U gate, along with an eigenstate |u\rangle of U with eigenvalue e^{i\varphi}.
We are promised that \varphi is of the form
\varphi
= 2\pi\frac{m}{2^n}
for some integers m and n.
Our task is to determine, using the fewest queries possible, the value of {\varphi}/{2\pi}={m}/{2^n}
Let’s work our way up to finding a circuit to solve this problem, starting with the following simple mathematical observation.
Since e^{i\varphi}=e^{i(\varphi+2\pi)}, we can assume m to be an integer between 0 and 2^n-1, which means that it has a binary representation of the form
m
= \sum_{i=1}^n m_i 2^{n-i}
for m_i\in\{0,1\}, and so
\varphi
= 2\pi\sum_{i=1}^n m_i 2^{-i}
This helps us rephrase the problem as “find the values of the m_i for i=1,\ldots,t”.
Now, rather than tackling the full problem, let’s try a much smaller modification of the original binary observable measurement problem: we have the same setup — a phase gate of unknown phase \varphi — but this time we are promised that \varphi is either 0 or \pi/2 (instead of 0 or \pi).
How can we adapt our original solution to find the phase value?
After some thought, you might see the trick: if we can apply the phase gate twice in a row, then we reduce the problem to the one we have already solved.
Indeed, if \varphi=0 then repeating it twice is the same as simply applying it once; if \varphi=\pi/2 then repeating it twice is the same as simply applying a phase gate of phase \pi.
Iterating this idea leads us to the first step of solving the general phase estimation problem, since if U|u\rangle=e^{i\varphi}|u\rangle then U^{2^{n-1}}|u\rangle=e^{2^{n-1}i\varphi}|u\rangle.
But
\begin{aligned}
2^{n-1}\varphi
&= 2^n\pi\frac{m}{2^n}
\\&= \pi m
\\&= \pi\sum_{i=1}^n m_i 2^{n-i}
\\&= \pi m_n + \pi\underbrace{\sum_{i=1}^{n-1}m_i2^{n-i}}_{\text{all divisible by }2}
\end{aligned}
and so, by the 2\pi-periodicity of e^{ix}, we see that
U^{2^{n-1}}|u\rangle
= e^{m_n\pi i}|u\rangle
and now we’re happy: m_n\in\{0,1\}, so this is an eigenvalue of U^{2^{n-1}} with phase 0 or \pi, reducing us to the original binary observable measurement problem that we have already solved by replacing U with U^{2^{n-1}}.
We have found the n-th bit m_n!

We’ve dealt with shrinking the distance between the two possible phases (if we have 0 and \pi/k for some k\in\mathbb{N} then we simply replace U by U^k), so now let’s look at the other way of modifying a pair of phases: shifting.
We have the same setup — a phase gate of unknown phase \varphi — but this time we are promised that \varphi is either -\pi/2 or \pi/2 (instead of 0 or \pi).
How can we adapt our original solution to find the phase value?
This time we just need to add \pi/2 to each of the phases, since then we’d end up back at 0 and \pi.
This means that we simply need to precede (or follow) the phase gate by the \pi/4-phase gate S=\left[\begin{smallmatrix}1&0\\0&i\end{smallmatrix}\right].
We already know how to find the value of m_n, so let’s use this to now find the value of m_{n-1}.
If we just try the same trick as before then we run into problems: it’s true that U^{2^{n-2}}|u\rangle=e^{2^{n-2}\varphi}|u\rangle, but
2^{n-2}\varphi
\equiv \pi m_{n-1}+\pi m_n/2 \ \mathrm{mod}\ 2\pi
so we have an annoying phase of \pi m_n/2 in the way.
However, we know that all we have to do now is to compensate for this by adding another phase gate:

Once we’ve got the value of m_{n-1} from this circuit, then we can simply apply the same idea to find m_{n-2}, m_{n-3}, and so on, until we have all the m_i for i=1,\ldots,n.
For example, the circuit to determine m_{n-3} (given than we already know m_n, m_{n-1}, and m_{n-2}) is

The entire process for determining the whole string m_1\ldots m_n, solving the scenario, can be written in a form that looks exactly how we expect: Hadamard–phase–Hadamard, modulo some subtle changes, which we will explain.
First register: n qubits. Second register: 1 qubit.
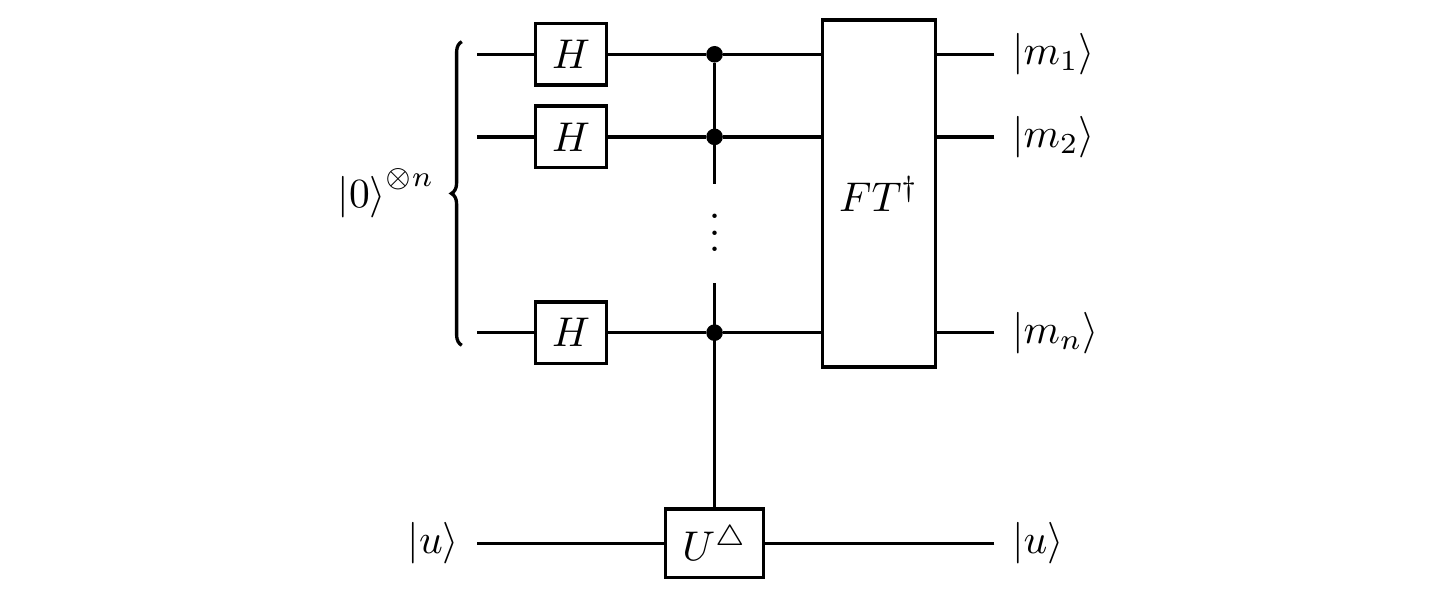
where U^\triangle is defined below, and FT^\dagger is defined in Section 10.9.
In this circuit, we write U^\triangle to mean the unitary that performs function evaluation as
|x\rangle|u\rangle
\longmapsto e^{i\varphi x}|x\rangle|u\rangle
or, in circuit language, the gate that acts on the i-th register as a controlled-U^{2^{n-i}} gate:
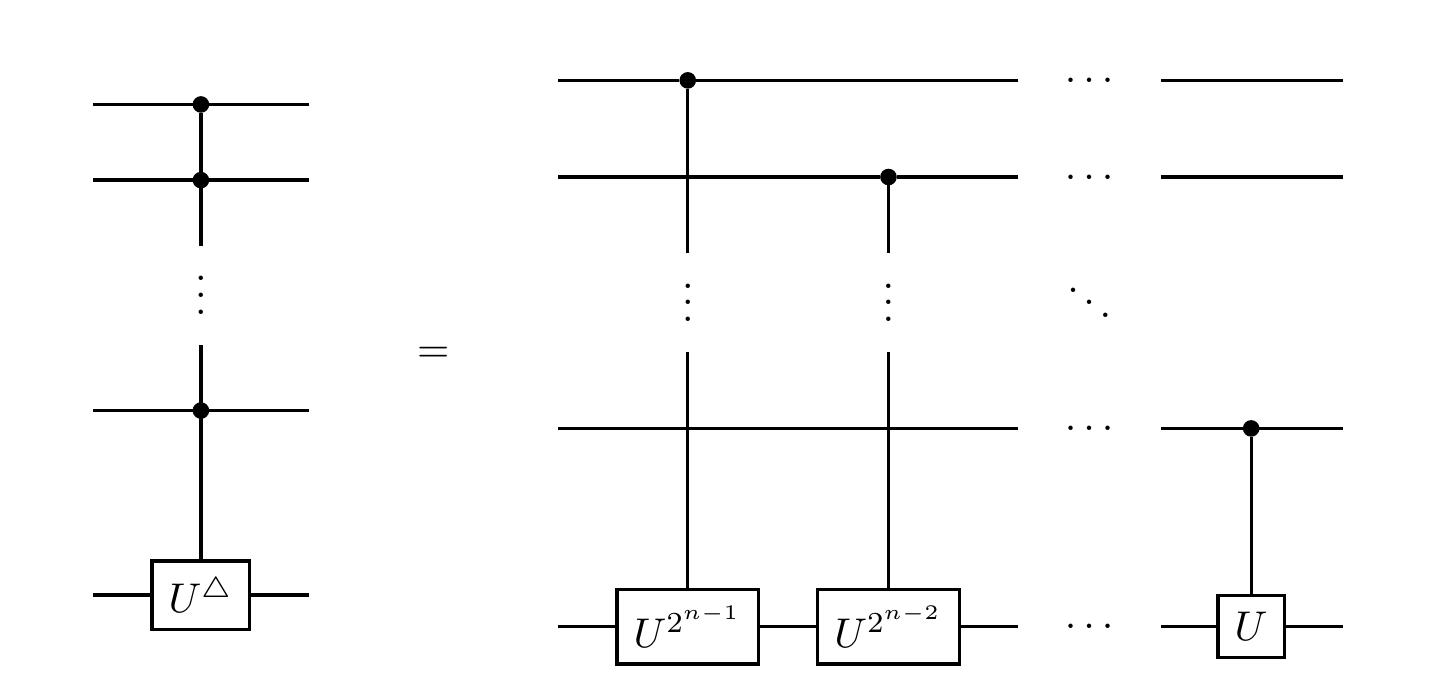
It is important to note, however, that we are sweeping something under the rug here.
If we can treat U^\triangle as an oracle itself, then this does indeed give an efficient solution, but if all we have access to is U then things are definitely not efficient: we are calling it 2^{n-1}+2^{n-2}+\ldots+2^0=2^n-1 many times, which is exponentially bad!
The only remaining part of the circuit to discuss is this mysterious FT^\dagger gate, but this deserves a section of its own.





