13.2 Towards error correction

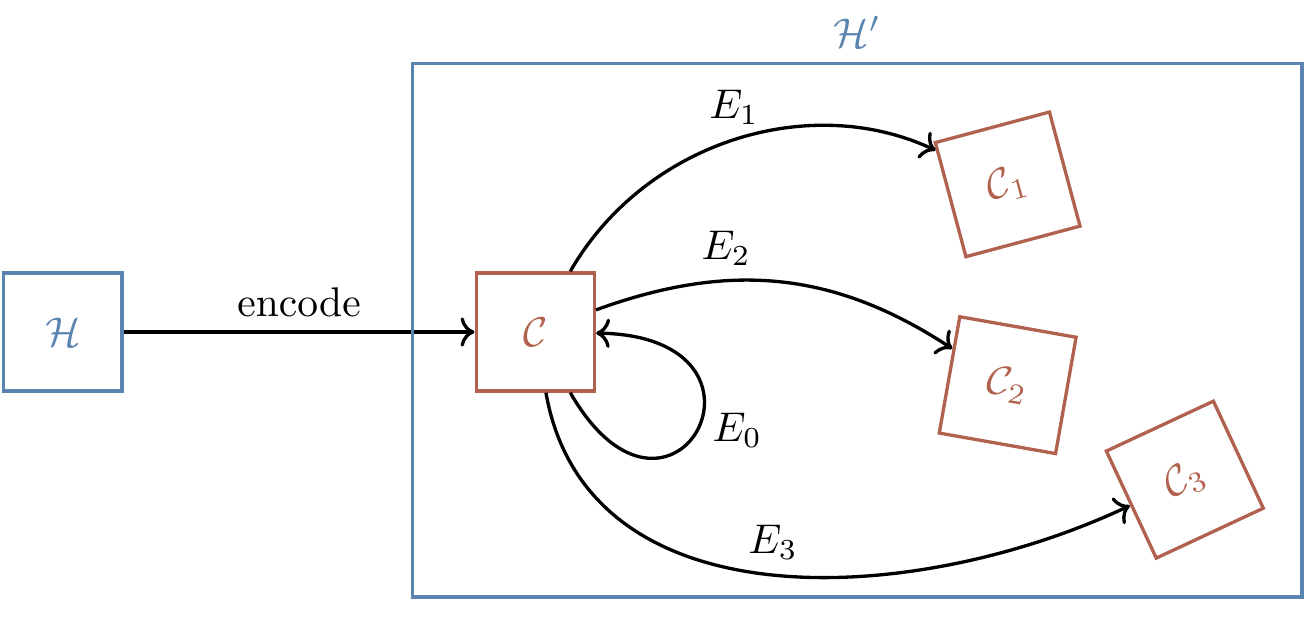
In Section 13.1, when Alice used a random choice of four isometries to produce a three-qubit output, notice how we can write \begin{aligned} V_{01} &= (\mathbf{1}\otimes\mathbf{1}\otimes X)V_{00} \\V_{01} &= (\mathbf{1}\otimes X\otimes\mathbf{1})V_{00} \\V_{01} &= (X\otimes\mathbf{1}\otimes\mathbf{1})V_{00} \end{aligned} and thus express all of the isometries in terms of V_{00}. In other words, rather than thinking of Alice as picking randomly between four different isometries, we can imagine that she always picks the encoding isometry V_{00}, and then some noisy process randomly applies one of the four actions \mathbf{1}, \mathbf{1}\mathbf{1}X, \mathbf{1}X\mathbf{1}, or X\mathbf{1}\mathbf{1}.

Correcting the isometry then corresponds to identifying which error happened, fixing it, and then removing the encoding: a process known as decoding. This is the format of error correction in a nutshell.

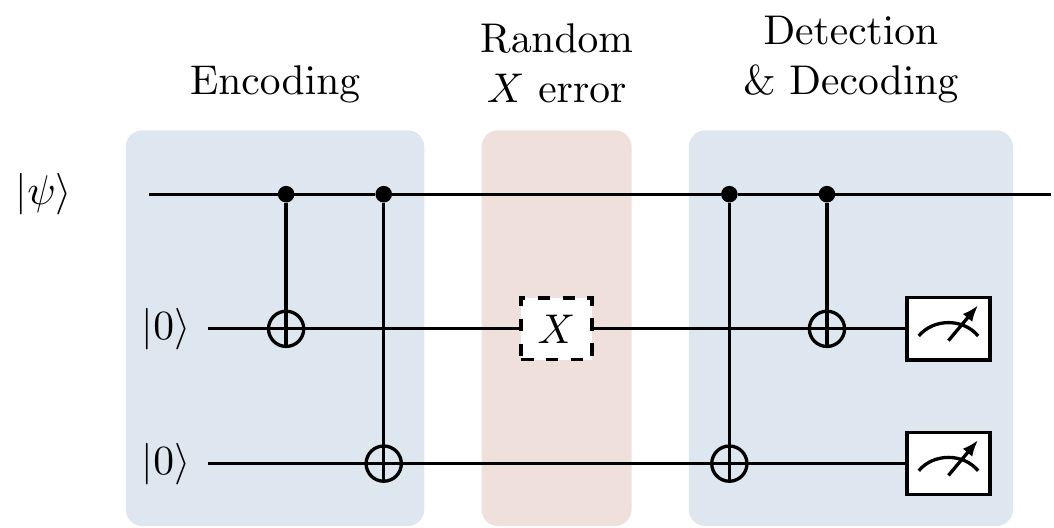
Quantum error correction can be thought of as a three-step process: encoding, transmitting through a noisy channel, and then detecting and decoding. We will give a more accurate depiction of an error correcting diagram, explaining what actually happens in the “detection & decoding portion” in Figure 13.7.

Figure 13.2: Quantum error correction can be thought of as a three-step process: encoding, transmitting through a noisy channel, and then detecting and decoding. We will give a more accurate depiction of an error correcting diagram, explaining what actually happens in the “detection & decoding portion” in Figure 13.7.

When we studied Pauli stabilisers in Section 7.2, we came across exactly the spaces of this example:

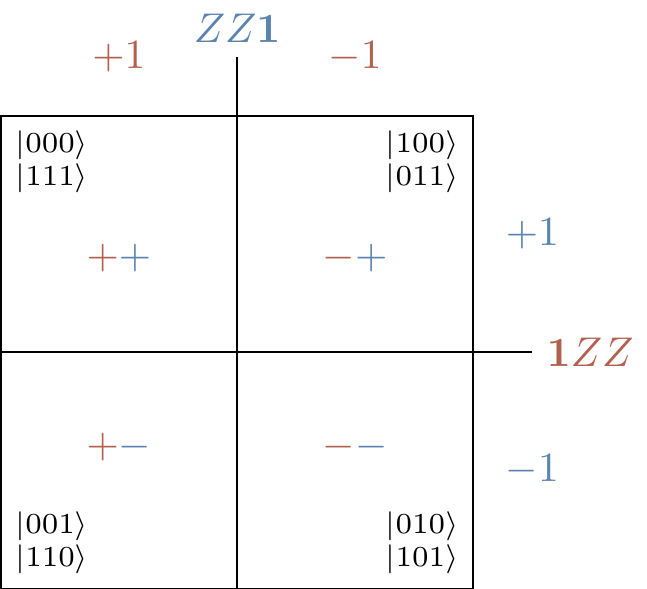
The stabiliser formalism gives us a very natural way of describing the error correcting code, along with its correction:

  • the codespace (i.e. the space with no error) is defined by the two stabilisers +ZZ\mathbf{1} and +\mathbf{1}ZZ
  • the error can be determined by measuring the value of these two stabilisers; we simply have to find which of the four possible errors gives the correct (anti-)commutation relations as specified by the measurement outcomes \pm1.

Generalising this idea further is the subject of Section 13.6.

If a set \{V_x\} of correctable isometries are related by V_x = U_xV_0 for some set of unitaries \{U_x\} with U_0=\mathbf{1}, then an encoding operation V_0 provides protection against the errors U_x.