6.6 Quantum randomness

The experimental violations of the CHSH inequality have shown us that there are situations in which the measurement outcomes are truly unknown the instant before the measurement is made, and so the answer must be “chosen” randomly. We can make use of this randomness in a number of different ways, the most obvious example of which being a random number generator. Indeed, we have already met one suitable implementation:

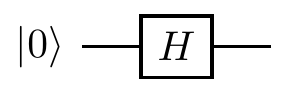
The state before measurement is (|0\rangle+|1\rangle)/\sqrt{2}, so the two possible outcomes occur with equal probability. This is a truly random number generator, not like the pseudorandom one that is used if you ask your computer for some random data.

This randomness generator works well as long as we know how it’s been built, i.e. that it really is just a Hadamard gate, that the input qubit really has been prepared in the state |0\rangle, and that the measurement device is accurate and honest. However, we don’t all have a Hadamard gate and a supply of prepared qubits lying around at home, so it seems likely that at some point we might have to buy or borrow such a device from a third party. But then how can we know that it really is doing what it promises, and not just supplying some pseudorandom numbers that might, for example, already be known to the manufacturer? This would render the device useless for cryptographic purposes! But not only do we want to know that this isn’t the case, we would also like the average user to be able to verify this for themselves, without having to know about the internal details. In other words, can we find a way of verifying the device via some analysis of just inputs and outputs? This is the question of device independence.

A protocol is device independent if its security doesn’t depend on trusting the devices on which it is implemented. In other words, it has no reliance on trusting the third party who supply you with the devices.

We can rule out one thing from the start, namely deterministic behaviour. If we behave deterministically then we have no hope, since the third party can take this into account and potentially find a way to always fool us. But there is another approach that we can try: rather than directly trying to verify the veracity of any given device, we can try to use it to turn a small amount of true randomness into a larger amount. This is the idea of randomness expansion.

Starting from an initial seed of private randomness (completely unknown to any other party), randomness expansion is the process of extending this to a larger amount of randomness that remains completely private.

Let’s consider a different device: one that produces pairs of qubits in singlet states and gives one of its qubits to Alice and one to Bob. If Alice then measures her qubit in the X basis, and Bob measures his in the Z basis (each keeping their outcomes private), they each obtain random bits that are independent of one another. However, this is only really true if the device truly is giving them singlet states, and not predetermined unentangled states. How can they test for this?

Using the idea of randomness expansion, let’s assume that they start with some shared random private seed: some m-bit string that only they know.135 They start by generating n of these putative singlet states, and publicly decide on some value 0<p<1. With this, they randomly select \lceil pn\rceil of the pairs to perform a CHSH test on. Each test requires two random bits (to determine Alice and Bob’s choice of measurement), so in total we will need the length m of their shared random private seed be roughly m \approx 2pn - pn\log_2 p - n(1-p)\log_2(1-p) where the \log terms are approximately how many bits are required to randomly choose the subset of pairs to test.

Why does this help? Well, if somebody has manipulated the device that produces the pairs, then they need to be sure that they haven’t altered the pairs that Alice and Bob are testing on. But they cannot know in advance which pairs that will be, and so they cannot risk manipulating anything.136

In the fraction p of pairs where a CHSH test is performed, we get at least 1 bit of randomness out: Alice’s measurement result is always chosen at random. In fact, Bob’s result will be partially correlated to Alice’s, so we should be able to extract some more randomness from this as well, but we ignore this possibility for the sake of simplicity. Thus in the end we create (2-p)n bits of randomness.

  1. Note that we’re pushing the problem somewhere else: how can they come up with this shared private seed in the first place? This is the problem of key distribution, and we’ll return to this again later.↩︎

  2. One can be much more quantitative about this by using Chernoff bounds for a simple strategy of “choose at random which pairs to manipulate”, but a full proof of security is much more involved than we would like to be here.↩︎