3.7 Remarks and exercises

3.7.1 Quantum bomb tester

You have been drafted by the government to help in the demining effort in a former war-zone.83 In particular, retreating forces have left very sensitive bombs in some of the sealed rooms. The bombs are configured such that if even one photon of light is absorbed by the fuse (i.e. if someone looks into the room), the bomb will go off. Each room has an input and output port which can be hooked up to external devices. An empty room will let light go from the input to the output ports unaffected, whilst a room with a bomb will explode if light is shone into the input port and the bomb absorbs even just one photon — see Figure 3.10.

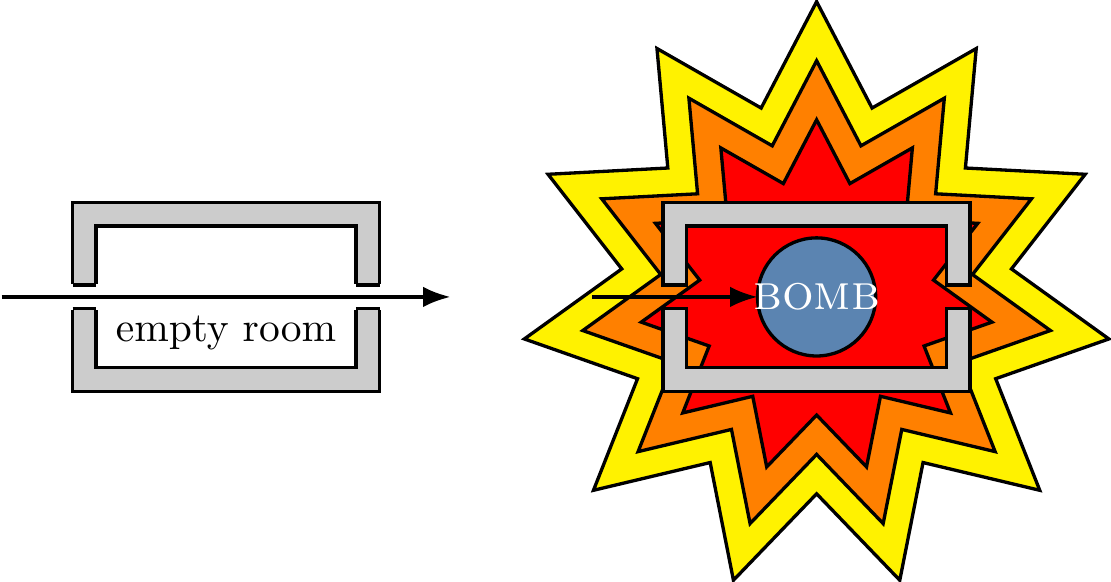
Left: the passage of a photon through an empty room. Right: the passage of a photon through a room containing a bomb.

Figure 3.10: Left: the passage of a photon through an empty room. Right: the passage of a photon through a room containing a bomb.

Your task is to find a way of determining whether a room has a bomb in it without blowing it up, so that specialised (limited and expensive) equipment can be devoted to defusing that particular room. You would like to know whether a particular room has a bomb in it with as much certainty as possible.

  1. To start with, consider the setup in Figure 3.11, where the input and output ports are hooked up in the lower arm of a Mach–Zehnder interferometer.
    1. Assume an empty room. Send a photon to input port |0\rangle. Which detector, at the output port, will register the photon?
    2. Now assume that the room does contain a bomb. Again, send a photon to input port |0\rangle. Which detector will register the photon and with which probability?
    3. Design a scheme that allows you — at least some of the time — to decide whether a room has a bomb in it without blowing it up. If you iterate the procedure, what is its overall success rate for the detection of a bomb without blowing it up?
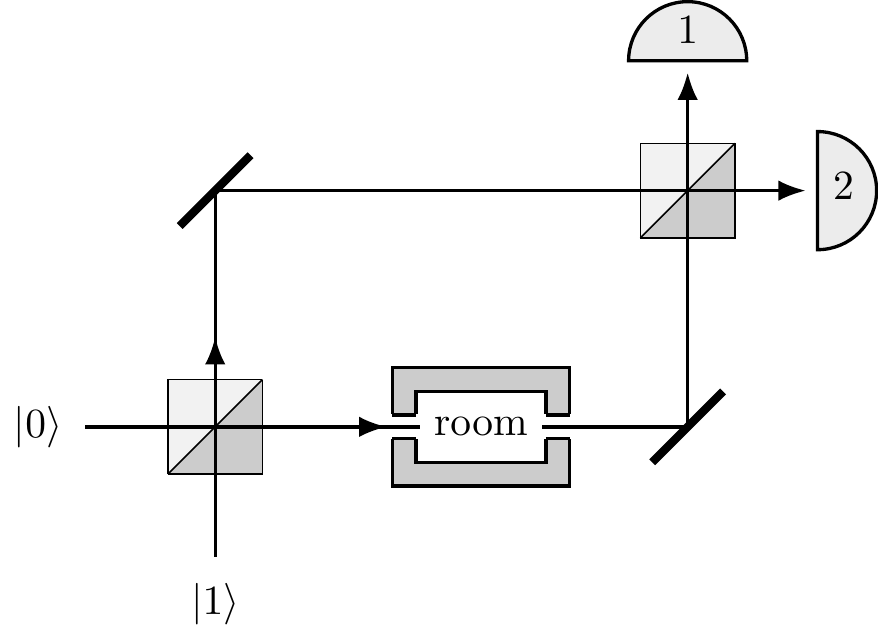
The Mach--Zehnder interferometer hooked up to the bomb-testing room.

Figure 3.11: The Mach–Zehnder interferometer hooked up to the bomb-testing room.

  1. Assume that the two beam splitters in the interferometer are different. Say the first beam-splitter reflects incoming light with probability R and transmits with probability T=1-R, but the second one transmits with probability R and reflects with probability T (that is, the two beam-splitters are asymmetric, but “inverse” to one another). Would the new setup improve the overall success rate of the detection of a bomb without blowing it up?

  2. There exists a scheme, involving many beam-splitters and something called the quantum Zeno effect, such that the success rate for detecting a bomb without blowing it up approaches 100%. Try to work it out, or find a solution on the internet.84

3.7.2 Orthonormal Pauli basis

Show that \{\mathbf{1},\sigma_x,\sigma_y,\sigma_z\} is an orthonormal basis of the space of complex (2\times 2) matrices with respect to the Hilbert-Schmidt product.

3.7.3 Pauli matrix expansion coefficients

Recall that any (2\times 2) complex matrix A has a unique expansion in the form \begin{aligned} A &= \begin{bmatrix} a_0 + a_z & a_x - i a_y \\a_x +i a_y & a_0 - a_z \end{bmatrix} \\&= a_0\mathbf{1}+ a_x \sigma_x + a_y \sigma_y + a_z \sigma_z \\&= a_0\mathbf{1}+ \vec{a}\cdot\vec{\sigma}. \end{aligned} \tag{$\star$} for some complex numbers a_0, a_x, a_y, and a_z.

  1. Show that the coefficients a_k (for k=x,y,z) are given by the inner product a_k = (\sigma_k|A) = \frac{1}{2}\operatorname{tr}\sigma_k A.

In these notes, we usually deal with matrices that are Hermitian (A=A^\dagger) or unitary (AA^\dagger=\mathbf{1}). It is easy to see that, if A is Hermitian, then a_0 and the three components of \vec{a} are all real. The (2\times 2) unitaries are usually parametrised as U = e^{i\varphi}\Big(u_0\mathbf{1}+ i(u_x\sigma_x + u_y\sigma_y + u_z\sigma_z)\Big) where e^{i\varphi} is an overall multiplicative phase factor, with \varphi real, and u_0 and the three components u_x, u_y, u_z are all real numbers.

  1. Show that the unitarity condition implies that u_0^2 + u_x^2 + u_y^2 + u_z^2 = 1 and show, using this parametrisation, that the determinant of U is e^{i2\varphi}.

3.7.4 Linear algebra of the Pauli vector

In what follows, we use the notation from our algebraic treatment of Pauli operators in Section 3.3, where we defined the Pauli vector \vec{\sigma}.

  1. Show that85 \frac{1}{2}\operatorname{tr}(\vec{a}\cdot\vec{\sigma})(\vec{b}\cdot\vec{\sigma}) = \vec{a}\cdot\vec{b}.

  2. Show that any \vec{n}\cdot\vec{\sigma} has eigenvalues \pm|\vec{n}|.

  3. Show that, if \vec{n}\cdot\vec{m}=0, then the operators \vec{n}\cdot\vec{\sigma} and \vec{m}\cdot\vec{\sigma} anticommute.

3.7.5 Matrix Euler formula

  1. Show that, if A^2=\mathbf{1}, then we can manipulate the power series expansion of e^{iA} into a simple expression: for any real \alpha, e^{i\alpha A} = (\cos\alpha)\mathbf{1}+ (i\sin\alpha)A.

  2. Show that any (2\times 2) unitary matrix U can be written, up to an overall multiplicative phase factor, as86 U = e^{i \theta \vec{n}\cdot\vec{\sigma}} = (\cos\theta)\mathbf{1}+ (i\sin\theta)\vec{n}\cdot\vec{\sigma}.

3.7.6 Special orthogonal matrix calculations

  1. Show that \operatorname{tr}\sigma_x\sigma_y\sigma_z = 2i.

  2. Let U be a unitary matrix, and write \vec{e}_x, \vec{e}_y, and \vec{e}_z to mean the unit vectors along the x-, y-, and z-axis, respectively. We define new unit vectors \vec{f}_x, \vec{f}_y, and \vec{f}_z by applying U to our existing unit vectors. Then U(\vec{e}_k\cdot\sigma_k)U^\dagger=U\sigma_kU^\dagger={\vec{f}_k}\cdot\vec\sigma. We already know that, in Euclidean space, this transformation is described by a (3\times 3) orthogonal matrix R_U. How are the three vectors \vec{f}_x, \vec{f}_y, and \vec{f}_z related to the entries in matrix R_U?

  3. Show that \begin{aligned} \operatorname{tr}\sigma_x\sigma_y\sigma_z &= \operatorname{tr}({\vec f_x}\cdot\vec\sigma)( {\vec f_y}\cdot\vec\sigma)({\vec f_z}\cdot\vec\sigma) \\&= 2i\det R_U \end{aligned} (which implies that \det R_U=1).

  4. Use the orthonormality of the Pauli basis along with Equation (\ddagger) to show that the elements of the matrix R=R_U can be expressed in terms of those of the matrix U, in the form R_{ij}=\frac{1}{2}\operatorname{tr}\left(\sigma_i U\sigma_j U^\dagger\right). Here, i and j take values in \{1,2,3\}, and \sigma_1\equiv\sigma_x, \sigma_2\equiv\sigma_y, \sigma_3\equiv\sigma_z.

3.7.7 Phase as rotation

  1. Show that87 the phase gate P_\varphi = \begin{bmatrix}1&0\\0&e^{i\varphi}\end{bmatrix} represents an anticlockwise rotation about the z-axis through the angle \varphi.

3.7.8 Calculating a Pauli rotation

  1. Express the Pauli rotation e^{i\sigma_y\pi/3} as a matrix.
  2. Give a decomposition of this rotation in the form88 R_Z(\alpha)HR_Z(\beta)HR_Z(\gamma) where R_Z(\theta) denotes a Pauli \sigma_z-rotation by angle \theta.

3.7.9 Geometry of the Hadamard

  1. Express the Hadamard gate H in terms of \vec{n}\cdot\vec{\sigma}, and show that \begin{aligned} HZH&=X \\HXH&=Z \\HYH&=-Y. \end{aligned}

  2. Show that the Hadamard gate H turns rotations about the x-axis into rotations about the z-axis, and vice versa. That is, \begin{aligned} H \left( e^{-i\frac{\varphi}{2}Z} \right) H &= e^{-i\frac{\varphi}{2}X} \\H \left( e^{-i\frac{\varphi}{2}X} \right) H &= e^{-i\frac{\varphi}{2}Z}. \end{aligned}

3.7.10 Swiss Granite Fountain

In the Singapore Botanic Gardens, there is a sculpture by Ueli Fausch called “Swiss Granite Fountain”. It is a spherical granite ball which measures 80cm in diameter and weighs 700kg, and is kept afloat by strong water pressure directed through a basal block. It is easy to set the ball in motion, and it keeps rotating in whatever way you start for a long time. Suppose you are given access to this ball only near the top, so that you can push it to make it rotate around any horizontal axis, but you don’t have enough of a grip to make it turn around the vertical axis. Can you make it rotate around the vertical axis anyway?

3.7.11 Dynamics in a magnetic field

A qubit initially in state |0\rangle is placed in a uniform magnetic field. The interaction between the field and the qubit is described by the Hamiltonian H = \omega \begin{bmatrix} 0 & - i \\i & 0 \end{bmatrix} where \omega is proportional to the strength of the field.89 What is the state of the qubit after time t=\pi/4\omega?

  1. This is a slightly modified version of a bomb-testing problem described by Avshalom Elitzur and Lev Vaidman in Quantum-mechanical interaction-free measurement, Found. Phys. 47 (1993), pp. 987–997.↩︎

  2. You can play around with this setup on the Quantum Flytrap Virtual Lab.↩︎

  3. Hint: you may find Exercise 2.14.9 helpful.↩︎

  4. Hint: the argument here is the same as the argument that e^{i\theta}=\cos\theta+i\sin\theta.↩︎

  5. Hint: it might be helpful to start with the \mathrm{SU}(2) version of the phase gate: \begin{aligned}P_\varphi&= e^{-i\frac{\varphi}{2}\sigma_z}\\&= \begin{bmatrix}e^{-i \frac{\varphi}{2}}& 0\\0 & e^{i \frac{\varphi}{2}}\end{bmatrix}\end{aligned} which gives R_{P_\varphi}=\begin{bmatrix}\cos \varphi & -\sin \varphi & 0\\\sin \varphi & \cos \varphi & 0\\0 & 0 & 1\end{bmatrix}↩︎

  6. Hint: recall Section 3.5.↩︎

  7. In Earth’s magnetic field, which is about 0.5 gauss, the value of \omega is of the order of 10^6 cycles per second.↩︎