5.8 Quantum teleportation
A wonderful fact, that sounds more like science fiction than actual science, is the following: an unknown quantum state can be teleported from one location to another. Consider the following circuit, which is built from a Bell state generator followed by an “offset” inverse Bell state generator:112
(Quantum teleportation).
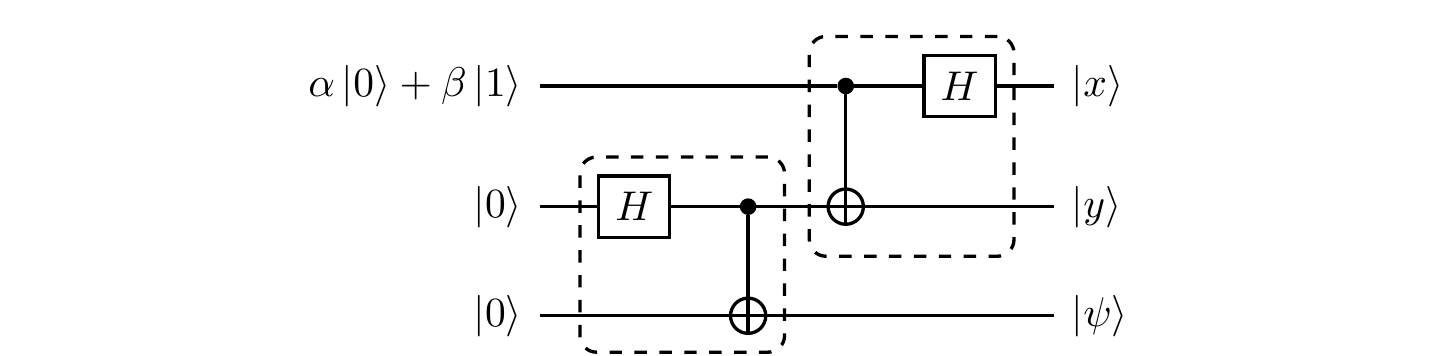
The first input qubit (counting from the top) is in some arbitrary state.
After the action of the part of the circuit in the first dashed box (counting from the left), the state of the three qubits reads113
If you understand how this circuit works114, then you are ready for quantum teleportation. Here is a dramatic version.
Suppose that three qubits, which all look very similar, are initially in the possession of an absent-minded Oxford student, Alice. The first qubit is in a precious quantum state and this state is needed urgently for an experiment in Cambridge. The other two qubits are entangled, in the
\Phi^+=|\psi_{00}\rangle state. Alice’s colleague, Bob, pops in to collect the qubit. Once he is gone, Alice realises that, by mistake, she gave him not the first but the third qubit: the one which is entangled with the second qubit.
The situation seems to be hopeless — Alice does not know the quantum state of the first qubit, and Bob is now miles away and her communication with him is limited to few bits. However, Alice and Bob are both very clever and they both diligently attended their “Introduction to Quantum Information Science” classes. Can Alice rectify her mistake and save Cambridge science?
…
Of course: Alice can teleport the state of the first qubit! She performs the Bell measurement on the first two qubits, which gives her two binary digits,
x andy . She then broadcastsx andy to Bob, who chooses the corresponding transformation, as in Equation (\circledast ), performs it, and recovers the original state.
This raises a natural “philosophical” question: what do we really mean by teleportation? A key part of this question is understanding what happens to our original qubit when we teleport it. Note that the actual physical electron (or whatever implementation of qubits we are using) does not suddenly move through space — what is teleported is the state of the qubit, but the argument can be made that if two qubits are entirely indistinguishable from one another by any measurements that we can make, then they really are “the same” in every way that matters, and so the qubit which now has the original qubit’s state “is the same as” the original qubit. As it turns out, this process necessarily destroys the original qubit’s state, as we now explain.
The first actual teleportation experiment was successfully achieved in 1997 (arXiv:quant-ph/9710013); in 2012 a record distance was set: an entangled photon pair was used to teleport a state 143 kilometres/88 miles (arXiv:1205.3909); in 2017, successful ground-to-satellite teleportation was achieved (arXiv:1707.00934). This is not science fiction!
But there is a fundamental question to ask: if the original state is destroyed, then how can we really verify that teleportation has taken place? We can’t compare the purportedly teleported state to the original one! The answer to this involves certain no-go theorems and statistical methods, where we can show that classical physics gives some strict upper bound on a certain fidelity, but which is clearly surpassed by these physical experiments. We will better explain the ideas behind these sorts of arguments later on, in Chapter 6, when we introduce Bell’s theorem.
Divide et impera, or “divide and conquer”: a good approach to solving problems in mathematics (and in life). Start with the smaller circuits in the dashed boxes, which we have just seen introduced above.↩︎
We don’t worry about writing the normalisation factors.↩︎
You can play around with this on the Quantum Flytrap Virtual Lab.↩︎