2.14 Remarks and exercises

2.14.1 One simple circuit

Let B be the matrix B = \frac{1}{\sqrt{2}} \begin{bmatrix} 1 & i \\i & 1 \end{bmatrix}.

1. Show that B is unitary.

2. Find the overall unitary corresponding to the circuit⁶³

   

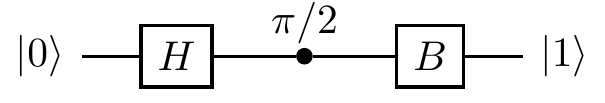
2.14.2 Change of basis

Write the state |\psi\rangle = \frac{3}{5}|0\rangle + \frac{4}{5}|1\rangle as a superposition of the states |\pm\rangle=(|0\rangle\pm|1\rangle)/\sqrt{2}. In other words, find \alpha,\beta\in\mathbb{C} such that |\psi\rangle = \alpha|+\rangle + \beta|-\rangle.

2.14.3 Operators as unitary matrices

Say we have a linear operator that acts on a qubit as follows: \begin{aligned} |0\rangle &\mapsto \alpha|0\rangle + \beta|1\rangle \\|1\rangle &\mapsto \beta^\star|0\rangle - \alpha^\star|1\rangle. \end{aligned}

1. Show that this linear operator is equal to M = \big(\alpha|0\rangle+\beta|1\rangle\big)\langle 0| + \big(\beta^\star|0\rangle-\alpha^\star|1\rangle\big)\langle 1| by calculating M|0\rangle and M|1\rangle.
2. If we pick the standard basis |0\rangle \equiv \begin{bmatrix} 1\\0 \end{bmatrix} \qquad |1\rangle \equiv \begin{bmatrix} 0\\1 \end{bmatrix} then what is the matrix representation of M?
3. Verify that M is unitary.

2.14.4 Completing an orthonormal basis

Imagine that some quantum system has four energy levels: |0\rangle, |1\rangle, |2\rangle, and |3\rangle. Consider the three orthonormal vectors \begin{aligned} |\psi_1\rangle &= \frac{1}{\sqrt{3}}(|0\rangle+|1\rangle+|2\rangle) \\|\psi_2\rangle &= \frac{1}{\sqrt{2}}(|0\rangle-|2\rangle) \\|\psi_3\rangle &= |3\rangle. \end{aligned} Find a vector |\psi_4\rangle such that \{|\psi_1\rangle,|\psi_2\rangle,|\psi_3\rangle,|\psi_4\rangle\} is an orthonormal basis.

2.14.5 Some sums of inner products

Let \{|v_1\rangle,\ldots,|v_N\rangle\} be an orthonormal basis. Evaluate the following:⁶⁴

1. \sum_{k=1}^{N-1} k^2 \langle v_{N-1}|v_k\rangle

2. \sum_{k=1}^{N-1} k^2 \langle v_N|v_k\rangle

3. \sum_{k=1}^N \langle v_{N-1}|v_k\rangle\langle v_k|v_{N-1}\rangle

4. \sum_{j,k=1}^{N-1} \langle v_j|v_k\rangle

2.14.6 Some circuit identities

1. Prove the following circuit identities, ignoring any global phase:

   

   

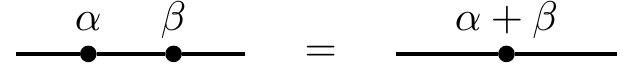
2. Using the above, find \theta_1 and \theta_2 such that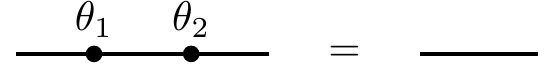

   

   

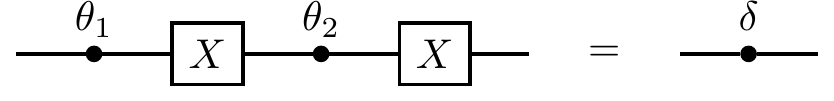
   for some value \delta.

3. We can think of the second identity in the previous question as an implementation of “if the two X gates are absent then do nothing; otherwise implement the phase gate P_\delta”. Given that unitary matrices are normal, adapt this circuit so that implements “if the two X gates are absent then do nothing; otherwise implement the unitary U” where U is a one-qubit unitary.

2.14.7 Unitaries preserve length

Let M be a linear operator that sends an orthonormal basis \{|u_1\rangle,\ldots,|u_N\rangle\} to a set of states \{|v_1\rangle,\ldots,|v_n\rangle\} where each |v_i\rangle is of length 1.

1. Show that the length of the vector M(|u_1\rangle+|u_2\rangle)/\sqrt{2} is \sqrt{1+\operatorname{Re}\langle v_1|v_2\rangle}.
2. Find a correctly normalised superposition |\psi\rangle=\lambda(\alpha|u_1\rangle+\beta|u_2\rangle) such that M|\psi\rangle is of length \sqrt{1+\operatorname{Im}\langle v_1|v_2\rangle}.
3. Using the above, show that, for all |\psi\rangle of length 1, the vector M|\psi\rangle is of length 1 if and only if M is unitary.

2.14.8 Unknown phase

Consider the usual quantum interference circuit:

Suppose you can control the input of the circuit and measure the output, but you do not know the phase shift \varphi introduced by the phase gate. You prepare input |0\rangle and register output |1\rangle. What can you say about \varphi?

Now you are promised that \varphi is either 0 or \pi. You can run the circuit only once to find out which of the two phases was chosen. Is it possible to then always correctly guess whether \varphi was 0 or \pi?

This problem forms the basis for a lot of material later on: most quantum algorithms build upon it. We will return to it again and again in Chapter 10.

2.14.9 One of the many cross-product identities

When working with three-dimensional geometry, the cross product of vectors is very useful, so here is an exercise to help you get used to working with it.

Let’s say we want to derive the identity⁶⁵ (\vec{a}\cdot\vec{\sigma})(\vec{b}\cdot\vec{\sigma}) = (\vec{a}\cdot\vec{b})\mathbf{1}+ i(\vec{a}\times \vec{b})\cdot \vec{\sigma}.

First, notice that the products of Pauli matrices can be written succinctly as \sigma_{i}\sigma_{j} = \delta _{ij}\mathbf{1}+ i\varepsilon_{ijk}\,\sigma _{k}, where \delta_{ij} is Kronecker delta (equal to 0 if i\neq j, and to 1 if i=j) and \varepsilon_{ijk} is the Levi-Civita symbol: \varepsilon_{ijk} = \begin{cases} +1 & {\text{if }}(i,j,k){\text{ is }}(1,2,3)\text{, }(2,3,1){\text{, or }}(3,1,2) \\-1 & {\text{if }}(i,j,k){\text{ is }}(3,2,1)\text{, }(1,3,2){\text{, or }}(2,1,3) \\\;\;\;0 & {\text{if }}i=j,{\text{ or }}j=k,{\text{ or }}k=i \end{cases} That is, \varepsilon _{ijk} is 1 if (i, j, k) is an even permutation of (1, 2, 3), it is -1 if it is an odd permutation, and it is 0 if any index is repeated. The Levi-Civita symbol is anti-symmetric, meaning when any two indices are changed, its sign alternates. Then recall that the scalar (dot) product and vector (cross) product of two Euclidean vectors \vec{a} and \vec{b} can be written, in terms of the components, as \begin{aligned} \vec{a}\cdot\vec{b} &= \sum_{i=1}^3 a_i b_i \\(\vec{a}\times\vec{b})_i &= \sum_{j,k=1}^3 \varepsilon_{ijk}a_jb_k. \end{aligned} The rest is rather straightforward: (\vec{a}\cdot\vec{\sigma})(\vec{b}\cdot\vec{\sigma}) = \sum_{i,j}a_i b_j\sigma_i\sigma_j = \ldots.

---

63. If you get the answer \begin{bmatrix}0&1\\i&0\end{bmatrix} then you performed the matrix multiplication in the wrong order!↩︎

64. All of your answers should be numbers (in fact, they’ll all even be integers).↩︎

65. Hint: all you need here are the Pauli matrices’ commutation and anticommutation relations, but it is instructive to derive the identity using the component notation, and below we give a sketch of how such a derivation would go.↩︎