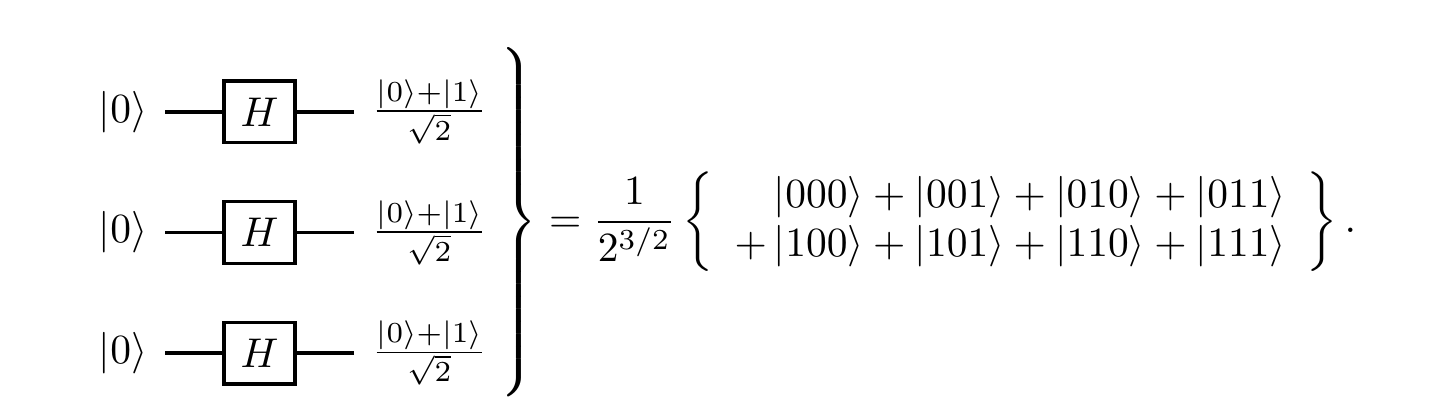More qubits, and binary representations
Let’s see how this formalism works for qubits.
The n-fold tensor product of vectors from the standard basis \{|0\rangle,|1\rangle\} represent binary strings of length n.
For example, for n=3,
\begin{aligned}
|0\rangle\otimes|1\rangle\otimes|1\rangle
& \equiv |011\rangle
\\|1\rangle\otimes|1\rangle\otimes|1\rangle
& \equiv |111\rangle.
\end{aligned}
A classical register (that is, a collection of bits) composed of three bits can store only one of these two binary strings at any time; a quantum register composed of three qubits can store both of them in a superposition.
Indeed, if we start with the state |011\rangle and apply the Hadamard gate to the first qubit (which is the same as applying H\otimes\mathbf{1}\otimes\mathbf{1}), then, given that linear combinations distribute over tensor products, we obtain
\begin{aligned}
|011\rangle
\overset{H\otimes\mathbf{1}\otimes\mathbf{1}}{\longmapsto}
&\frac{1}{\sqrt{2}} \big(|0\rangle + |1\rangle\big) \otimes|1\rangle\otimes|1\rangle
\\=
&\frac{1}{\sqrt{2}} \big(|011\rangle + |111\rangle\big).
\end{aligned}
In fact, we can even prepare this register in a superposition of all eight possible binary strings of length 3 at once: if we apply the tensor product operation H\otimes H\otimes H to the state |0\rangle\otimes|0\rangle\otimes|0\rangle = |000\rangle then we get
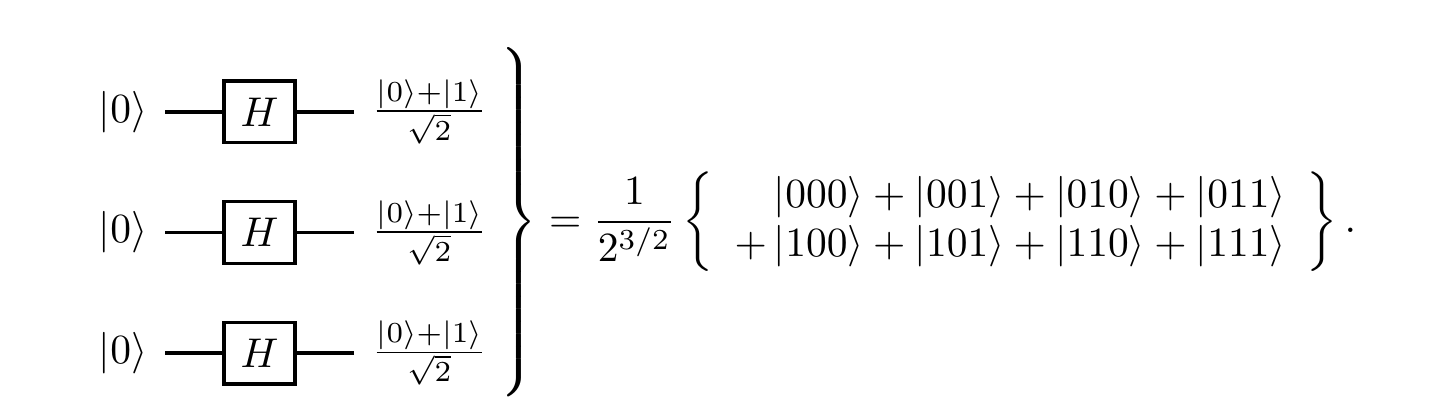
The resulting state is exactly a superposition of all binary strings of length 3, and can also be written as
\frac{1}{\sqrt{2}} \big(|0\rangle + |1\rangle\big)
\otimes
\frac{1}{\sqrt{2}} \big(|0\rangle + |1\rangle\big)
\otimes
\frac{1}{\sqrt{2}} \big(|0\rangle + |1\rangle\big).
In general, the tensor product operation H^{\otimes n}, which means “apply the Hadamard gate to each of your n qubits”, is known as the Hadamard transform, and it maps product states to product states.
Like the Hadamard gate in the typical quantum interference circuit, the Hadamard transform opens (and closes) multi-qubit interference.
One final note is on notation, or maybe more a shift of point-of-view.
We have just explained how applying the Hadamard transform to n qubits gives us the equally weighted superposition of all binary strings of length n.
But rather than writing them as binary strings, we could consider the decimal number represented by each string.
This means we switch from considering all binary strings of length n to considering all natural numbers from 0 to N-1, where N=2^n.
For example, with n=3 qubits, we could either write
\frac{1}{\sqrt{2^n}} \sum_{x\in\{0,1\}^n} |x\rangle
or instead switch to the decimal approach with N=2^n=8 and write
\frac{1}{\sqrt{N}} \sum_{x=0}^{N-1} |x\rangle
so that we are writing |7\rangle to mean |111\rangle, and |3\rangle to mean |011\rangle, and |0\rangle to mean |000\rangle, and so on.