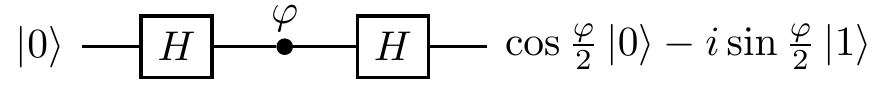Universality, again
Although this may all seem tediously abstract, it is surprisingly useful.
Take another look at the single-qubit interference circuit
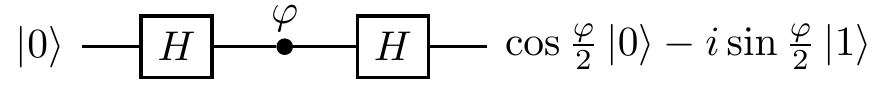
and the corresponding sequence of unitary operations
\begin{aligned}
H \left(
e^{-i\frac{\varphi}{2}Z}
\right) H
&= e^{-i\frac{\varphi}{2}X}
\\&= \begin{bmatrix}
\cos\varphi/2 & -i\sin\varphi/2
\\-i\sin\varphi/2 & \cos\varphi/2
\end{bmatrix}
\end{aligned}
The single-qubit interference circuit has a simple geometrical meaning: it shows how a rotation about the z-axis, induced by the phase gate P_\varphi, is turned, by the two Hadamard gates, into a rotation about the x-axis.
Now, take a look at this circuit:
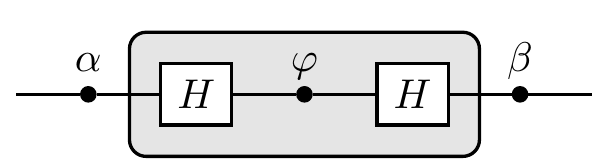
What does it represent?
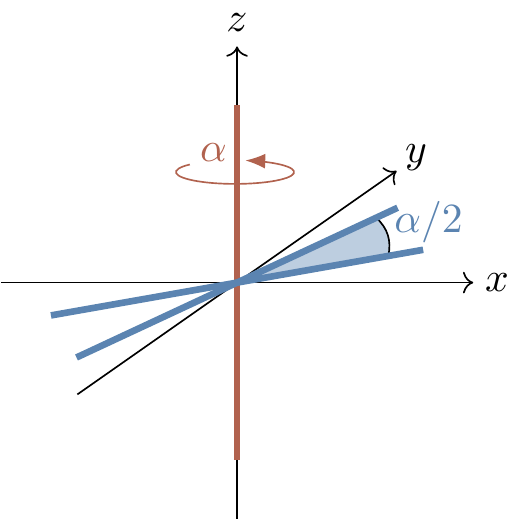
The central part is a rotation by \varphi about the x-axis, sandwiched between two rotations about the z-axis.
Recall our previous discussion (Section 2.12) about a universal set of gates: any rotation in the Euclidean space can be performed as a sequence of three rotations: one about z-axis, one about x-axis, and one more about the z-axis.
In this context, this implies that any unitary U, up to a global phase factor, can be written as
\begin{aligned}
U(\alpha, \beta, \varphi)
&= e^{-i\frac{\beta}{2}Z} e^{-i\frac{\varphi}{2}X} e^{-i\frac{\alpha}{2}Z}
\\&= \begin{bmatrix}
e^{-i\left(\frac{\alpha+\beta}{2}\right)}\cos\frac{\varphi}{2}
& ie^{i\left(\frac{\alpha-\beta}{2}\right)}\sin\frac\varphi{2}
\\ie^{-i\left(\frac{\alpha-\beta}{2}\right)}\sin\frac\varphi{2}
& e^{i\left(\frac{\alpha+\beta}{2}\right)}\cos\frac\varphi{2}
\end{bmatrix}.
\end{aligned}
That is, once you are given a pair of Hadamard gates and an infinite supply of phase gates (so that you can choose the three phases you need) you can construct an arbitrary unitary operation on a single qubit.
It is important to note that the two axes in question, z and x, do not have any special status, geometrically speaking — if we have rotations about any two orthogonal axes then we can create any one-qubit unitary that we want.
Now consider the following circuit:

where both A and B are unitary operations.
We claim that any unitary U can be represented in this form, for some A and B.
Again, we can prove this geometrically.
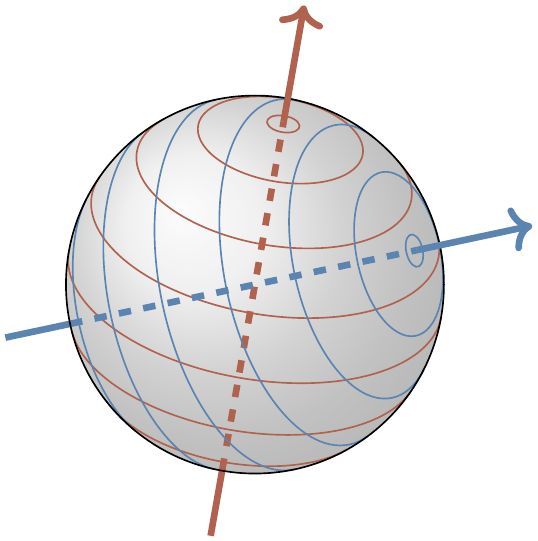
The circuit represents two rotations by 180^\circ about the two axes obtained by rotating the z-axis via unitaries A and B, respectively.
Any rotation in the three-dimensional space is the composition of two rotations by 180^\circ, as shown in Figure 3.9.
The resulting axis of rotation is perpendicular to the two axes about which rotations by 180^\circ are performed, and the angle of the composed rotation is twice the angle between the two axes.