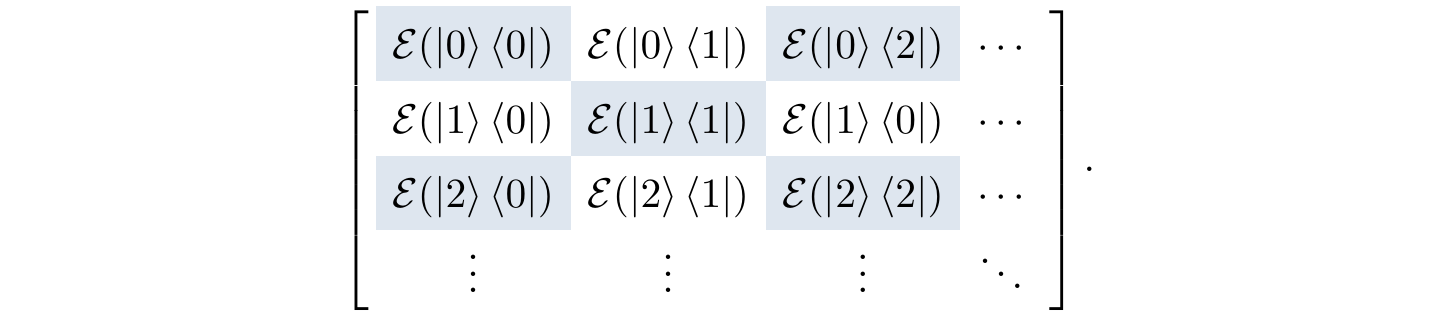Channel-state duality
Suppose that \dim\mathcal{H}=d and \dim\mathcal{H}'=d', and pick a basis for each space.
Now any linear map \mathcal{E}\colon\mathcal{B}(\mathcal{H})\to\mathcal{B}(\mathcal{H'}) can be completely characterised by its action on the d^2-many basis matrices |i\rangle\langle j| of \mathcal{B}(\mathcal{H}) (where i,j\in\{1,2\ldots,d\}), i.e. for any density operator \rho on \mathcal{H} we have
\mathcal{E}(\rho)
= \mathcal{E}\left(\sum_{i,j=1}^d\rho_{ij} |i\rangle\langle j|\right)
= \sum_{i,j=1}^d\rho_{ij}\mathcal{E}(|i\rangle\langle j|).
\tag{$\natural$}
We can now tabulate the (d\times d)-many (d'\times d') matrices \mathcal{E}(|i\rangle\langle j|) in \mathcal{H}' by forming a bigger (dd'\times dd') block matrix in \mathcal{H}\otimes\mathcal{H}':
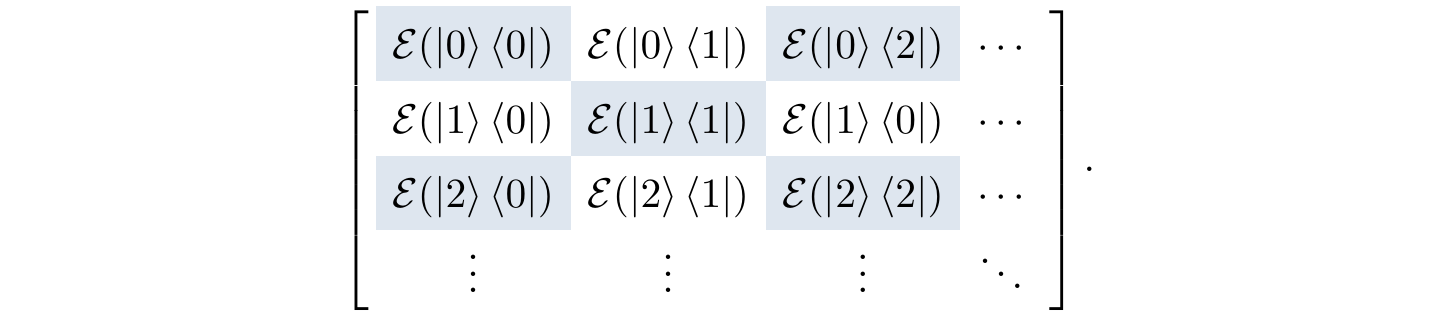
After scaling by a factor of \frac{1}{d}, we call this block matrix \widetilde{\mathcal{E}}\in\mathcal{B}(\mathcal{H}\otimes\mathcal{H}') the Choi matrix of \mathcal{E}.
The Choi matrix is essentially another way of representing a linear map \mathcal{E}\colon\mathcal{B}(\mathcal{H})\to\mathcal{B}(\mathcal{H'}), since if you are given the Choi matrix \widetilde{\mathcal{E}} of \mathcal{E} and you want to evaluate \mathcal{E}(\rho), then you simply follow Equation (\natural), taking the values of \mathcal{E}(|i\rangle\langle j|) from the Choi matrix.
We can write this more formally as follows.
The Choi matrix \widetilde{\mathcal{E}} of a linear map \mathcal{E}\colon\mathcal{B}(\mathcal{H})\to\mathcal{B}(\mathcal{H'}) satisfies
\frac{1}{d}\mathcal{E}(\rho)
= (\operatorname{tr}\otimes\mathbf{1})\left[(\rho^T\otimes\mathbf{1}_{d'\times d'})\widetilde{\mathcal{E}}\right]
for all density matrices \rho in \mathcal{B}(\mathcal{H}), where d=\dim\mathcal{H}.
The expression above may look baffling at first glance, but this is often the case when we turn something conceptually obvious into more compact mathematical notation.
In order to gain some intuition here, recall that, for matrices A and B,
\operatorname{tr}A^T B = \sum_{i,j} A_{ij}B_{ij}.
If we take A and B to be the block matrices \rho\otimes\mathbf{1} and \widetilde{\mathcal{E}}, respectively, then we can use this to show that
(\operatorname{tr}\otimes\mathbf{1})\left[(\rho^T\otimes\mathbf{1})\widetilde{\mathcal{E}}\right]
= \frac{1}{d}\sum_{i,j}\rho_{ij}\mathcal{E}(|i\rangle\langle j|).
This gives us a one-to-one correspondence between linear maps \mathcal{E}\colon\mathcal{B}(\mathcal{H})\to\mathcal{B}(\mathcal{H}') and matrices \widetilde{\mathcal{E}} acting on the tensor product \mathcal{H}\otimes\mathcal{H}', known as the Choi–Jamiołkowski isomorphism \mathcal{E}\mapsto\widetilde{\mathcal{E}}.
The correspondence between linear maps \mathscr{B}(\mathcal{H})\to\mathscr{B}(\mathcal{H'}) and operators in \mathscr{B}(\mathcal{H}\otimes\mathcal{H'}), known as the Choi–Jamiołkowski isomorphism (or channel-state duality in the specific setting of quantum information), is another example of a well known correspondence between vectors in \mathcal{H}_{\mathcal{A}}\otimes\mathcal{H}_{\mathcal{B}} and operators \mathscr{B}(\mathcal{H}_{\mathcal{A}}^\star,\mathcal{H}_{\mathcal{B}}) or \mathscr{B}(\mathcal{H}_{\mathcal{B}}^\star,\mathcal{H}_{\mathcal{A}}).
Take a tensor product vector in |a\rangle\otimes|b\rangle\in \mathcal{H}_{\mathcal{A}}\otimes\mathcal{H}_{\mathcal{B}}.
Then it defines natural maps in \mathscr{B}(\mathcal{H}_{\mathcal{A}}^\star,\mathcal{H}_{\mathcal{B}}) and \mathscr{B}(\mathcal{H}_{\mathcal{B}}^\star,\mathcal{H}_{\mathcal{A}}), via
\begin{aligned}
\langle x|
&\longmapsto \langle x|a\rangle|b\rangle
\\\langle y|
&\longmapsto |a\rangle\langle y|b\rangle
\end{aligned}
for any linear forms \langle x|\in\mathcal{H}^\star_A and \langle y|\in\mathcal{H}^\star_B.
We then extend this construction (by linearity) to any vector in \mathcal{H}_{\mathcal{A}}\otimes\mathcal{H}_{\mathcal{B}}.
These isomorphisms are canonical: they do not depend on the choice of any bases in the vectors spaces involved.
However, some care must be taken when we want to define correspondence between vectors in \mathcal{H}_{\mathcal{A}}\otimes\mathcal{H}_{\mathcal{B}} and operators in \mathscr{B}(\mathcal{H}_{\mathcal{A}},\mathcal{H}_{\mathcal{B}}) or \mathscr{B}(\mathcal{H}_{\mathcal{B}},\mathcal{H}_{\mathcal{A}}).
For example, physicists like to “construct” \mathscr{B}(\mathcal{H}_{\mathcal{B}},\mathcal{H}_{\mathcal{A}}) in a deceptively simple way:
|a\rangle|b\rangle \longleftrightarrow |a\rangle\langle b|.
Flipping |b\rangle and switching from \mathcal{H}_{\mathcal{B}} to \mathcal{H}^\star_B is an anti-linear operation (since it involves complex conjugation).
This is fine when we stick to a specific basis |i\rangle|j\rangle and use the ket-flipping approach only for the basis vectors.
This means that, for |b\rangle=\sum_j\beta_j|j\rangle, the correspondence looks like
|i\rangle|b\rangle \longleftrightarrow \sum_j \beta_j |i\rangle\langle j|
and not like
|i\rangle|b\rangle \longleftrightarrow |i\rangle\langle b|
= \sum_j \beta^\star_j |i\rangle\langle j|.
This isomorphism is non-canonical: it depends on the choice of the basis.
But it is still a pretty useful isomorphism!
The Choi–Jamiołkowski isomorphism is of this kind (i.e. non-canonical) — it works in the basis in which you express a maximally mixed state |\Omega\rangle=\sum_i|i\rangle|i\rangle.
Mathematically, it is not too surprising that the matrix elements of an operator on a tensor product can be reorganised and reinterpreted as the matrix elements of an operator between operator spaces.
What is interesting, and perhaps not so obvious, however, is that the positivity conditions for maps correspond exactly to conditions on their Choi matrices under this correspondence.
That is, this one-to-one correspondence between linear maps \mathcal{E}\colon\mathcal{B}(\mathcal{H})\to\mathcal{B}(\mathcal{H}') and matrices \widetilde{\mathcal{E}} acting on the tensor product \mathcal{H}\otimes\mathcal{H}' descends to a one-to-one correspondence between quantum channels and some specific family of matrices (which we will shortly discuss).
In other words, we can classify quantum channels as being exactly those linear maps that have a certain image under the Choi–Jamiołkowski isomorphism!
In order to see this, let us express the Choi matrix as the result of \mathbf{1}\otimes\mathcal{E} acting on the maximally mixed state
|\Omega\rangle\coloneqq\frac{1}{\sqrt{d}}\sum_{i=1}^d|i\rangle|i\rangle
in \mathcal{H}\otimes\mathcal{H}.
The Choi matrix \widetilde{\mathcal{E}} of a linear map \mathcal{E}\colon\mathcal{B}(\mathcal{H})\to\mathcal{B}(\mathcal{H'}) is given by
\widetilde{\mathcal{E}}
= (\mathbf{1}_{d\times d}\otimes\mathcal{E})|\Omega\rangle\langle\Omega|
= \frac{1}{d} \sum_{i,j} |i\rangle\langle j|\otimes\mathcal{E}(|i\rangle\langle j|)
where d=\dim\mathcal{H}.
Pictorially, we might represent this by something like

In this form, we can see right away that, if \mathcal{E} is a quantum channel, then \widetilde{\mathcal{E}} is a density matrix.
In fact, not just any density matrix: the first subsystem of the maximally entangled state |\Omega\rangle is initially maximally, and remains maximally mixed, since we apply the identity operator, and so (\mathbf{1}\otimes\operatorname{tr})\widetilde{\mathcal{E}}=\frac{1}{d}\mathbf{1}.
The converse is also true: any density matrix \widetilde{\mathcal{E}} such that (\mathbf{1}\otimes\operatorname{tr})\widetilde{\mathcal{E}}=\frac{1}{d}\mathbf{1} defines a quantum channel, i.e. a completely positive trace-preserving map.
This is just one example of how, in general, the Choi–Jamiołkowski isomorphism provides a simple way of studying linear maps on operators by means of inspecting their Choi matrices.
Let \widetilde{\mathcal{E}} be the Choi matrix of a linear map \mathcal{E}\colon\mathcal{B}(\mathcal{H})\to\mathcal{B}(\mathcal{H'}).
Then
- \mathcal{E} is completely positive if and only if \widetilde{\mathcal{E}} is positive semi-definite.
- \mathcal{E} is trace preserving if and only if (\mathbf{1}\otimes\operatorname{tr})\widetilde{\mathcal{E}}=\frac{1}{d}\mathbf{1}.
- \mathcal{E} sends the identity operator to the identity operator if and only if (\operatorname{tr}\otimes\mathbf{1})\widetilde{\mathcal{E}}=\frac{1}{d}\mathbf{1}.
- \mathcal{E} sends Hermitian operators to Hermitian operators and only if \widetilde{\mathcal{E}} is Hermitian.
We shall prove the first two of these correspondences here, and leave the last two as an exercise.
Let’s start with complete positivity, since one direction is much easier: if \mathcal{E} is a completely positive map, then its extension \mathbf{1}\otimes\mathcal{E} maps |\Omega\rangle\langle\Omega| to a positive semi-definite matrix, and so \widetilde{\mathcal{E}} is positive semi-definite.
The converse is less immediate.
If \widetilde{\mathcal{E}} is positive semi-definite, then its eigenvalues p_k are non-negative, and we can write its spectral decomposition as
\widetilde{\mathcal{E}}
= \sum_k p_k|\psi_k\rangle\langle\psi_k|
= \sum_k |\widetilde{\psi}_k\rangle\langle\widetilde{\psi}_k|
where the vectors |\widetilde{\psi}_k\rangle=\sqrt{p_k}|\psi_k\rangle are pairwise orthogonal but not normalised.
Each of the vectors |\widetilde{\psi}_k\rangle can be written as
|\widetilde{\psi}_k\rangle
= (\mathbf{1}\otimes E_k)|\Omega\rangle
for some operator E_k (Exercise 9.12.15).
This means that
\begin{aligned}
\widetilde{\mathcal{E}}
&= \sum_k |\widetilde{\psi}_k\rangle\langle\widetilde{\psi}_k|
\\&= \sum_k (\mathbf{1}\otimes E_k)|\Omega\rangle\langle\Omega|(\mathbf{1}\otimes E_k^\dagger)
\\&= \frac{1}{d}\sum_{i,j} \left(|i\rangle\langle j|\otimes\underbrace{\sum_k E_k\langle i||j\rangle E_k^\dagger}_{\mathcal{E}(|i\rangle\langle j|)}\right).
\end{aligned}
Comparing this last expression with the definition of \widetilde{\mathcal{E}}, we conclude that \mathcal{E} is of the form
\mathcal{E}(\rho)
= \sum_k E_k\rho E_k^\dagger
which is a completely positive map in Kraus form (though not necessarily trace preserving, since we do not require that \sum_k E_k E_k^\dagger=\mathbf{1}).
For the trace-preserving correspondence, note first of all that, if \mathcal{E} is trace preserving, then
\begin{aligned}
(\mathbf{1}\otimes\operatorname{tr})\widetilde{\mathcal{E}}
&= \frac{1}{d}\sum_{i,j} |i\rangle\langle j| \underbrace{\operatorname{tr}\mathcal{E}(|i\rangle\langle j|)}_{\delta_{ij}}
\\&= \frac{1}{d}\sum_i|i\rangle\langle i|
\\&= \frac{1}{d}\mathbf{1}.
\end{aligned}
Conversely, for any operator \rho in \mathcal{B}(\mathcal{H}), we have already seen that
\frac{1}{d}\operatorname{tr}\mathcal{E}(\rho)
= (\operatorname{tr}\otimes1)\left[(\rho^T\otimes\mathbf{1})\widetilde{\mathcal{E}}\right]
and so, tracing over \mathcal{H}' by applying \mathbf{1}\otimes\operatorname{tr}, we see that
\operatorname{tr}\mathcal{E}(\rho)
= (\mathbf{1}\otimes\operatorname{tr})\left[d(\operatorname{tr}\otimes1)\left[(\rho^T\otimes\mathbf{1})\widetilde{\mathcal{E}}\right]\right]
which rearranges to give
\begin{aligned}
\operatorname{tr}\mathcal{E}(\rho)
&= d(\operatorname{tr}\otimes\operatorname{tr})\left[(\rho^T\otimes\mathbf{1})\widetilde{\mathcal{E}}\right]
\\&= d(\operatorname{tr}\otimes\mathbf{1})\left[\rho^T(\mathbf{1}\otimes\operatorname{tr})\widetilde{\mathcal{E}}\right]
\end{aligned}
by using the fact that (\operatorname{tr}\otimes\operatorname{tr})[(A\otimes\mathbf{1})C]=(\operatorname{tr}\otimes\mathbf{1})[A(\mathbf{1}\otimes\operatorname{tr})C], which is just another way of writing the defining property of the partial trace: \operatorname{tr}_{\mathcal{AB}}(A\otimes\mathbf{1})C=\operatorname{tr}_{\mathcal{A}}(A\operatorname{tr}_{\mathcal{B}}C).
So if (\mathbf{1}\otimes\operatorname{tr})\widetilde{\mathcal{E}}=\frac{1}{d}\mathbf{1}, then
\operatorname{tr}\mathcal{E}(\rho)
= \operatorname{tr}\rho^T
= \operatorname{tr}\rho
and so \mathcal{E} is trace preserving.
Note that we have already used this defining property of the partial trace when calculating the expectation value of an observable A that pertains only to a subsystem \mathcal{A} of a bipartite system \mathcal{AB} described by some density operator \rho_{\mathcal{AB}}, noting that \operatorname{tr}[(A\otimes\mathbf{1})\rho_{\mathcal{AB}}]=\operatorname{tr}[A\rho_{\mathcal{A}}], where \rho_{\mathcal{A}}=\operatorname{tr}_\mathcal{B}\rho_{\mathcal{AB}}.
In particular then, completely positive trace-preserving maps (quantum channels) have Choi matrices that are positive semi-definite and such that their partial trace gives the maximally mixed state \frac{1}{d}\mathbf{1}, and we have just shown that the converse is true.
Channel–state duality.
The following three things are all equivalent to one another:
- quantum channels (i.e. linear maps that can be written in Stinespring or Kraus form)
- completely positive trace-preserving (CPTP) maps
- linear maps \mathcal{E} whose Choi matrix \widetilde{\mathcal{E}} is positive semi-definite and such that (\mathbf{1}\otimes\operatorname{tr})\widetilde{\mathcal{E}}=\frac{1}{d}\mathbf{1}.
Furthermore, all completely positive maps admit a Kraus decomposition \rho\mapsto\sum_k E_k\rho E_k^\dagger, and these Kraus operators can be obtained from the spectral decomposition of the corresponding Choi matrix.
Given the Kraus decomposition, if we also want the map to be trace preserving, then we must additional require that the Kraus operators satisfy \sum_k E_k^\dagger E_k=\mathbf{1}.