Pauli stabilisers
The stabiliser (or stabilizer, if you like) formalism is an elegant technique that is often used to describe vectors and subspaces.
Suppose you want to specify a particular vector in a Hilbert space.
The most conventional way to do this would be to pick a basis and then list the coordinate components of the vector.
But we could instead list a set of operators that leave this vector invariant.
More generally, we can define a vector subspace (rather than just a single vector, which corresponds to a 1-dimensional subspace: its span) by giving a list of operators that fix this subspace.
Such operators are called stabilisers.
We say that an operator S stabilises a (non-zero) state |\psi\rangle if S|\psi\rangle=|\psi\rangle, and we then call |\psi\rangle a stabiliser state.
We say that S stabilises a subspace V if S stabilises every state in V, and we call the largest subspace V_S that is stabilised by S the stabiliser subspace.
In other words, an operator S stabilises a state |\psi\rangle (or the state is fixed by the operator) if |\psi\rangle is an eigenstate of S with eigenvalue 1.
It is very important to note that here we have to pay attention to the global phase factor: if S|\psi\rangle=-|\psi\rangle then we do not say that S stabilises |\psi\rangle, even though |\psi\rangle and -|\psi\rangle describe the same quantum state.
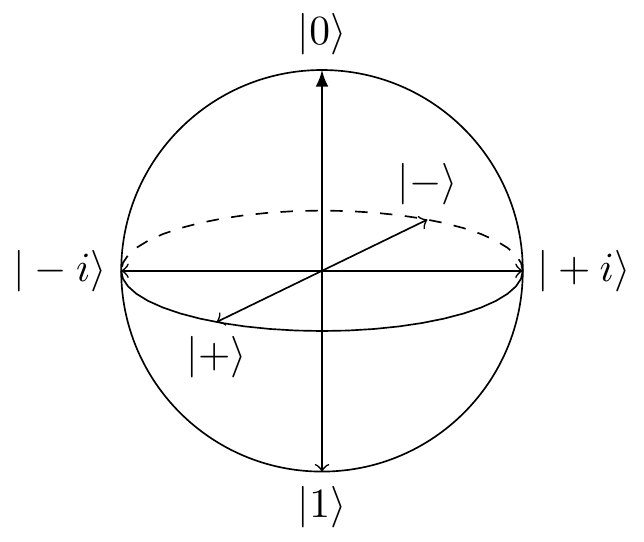
For example, we can look at states stabilised by the Pauli operators with factors \pm1:
\begin{aligned}
Z\text{ stabilises }|0\rangle
&\qquad-Z\text{ stabilises }|1\rangle
\\Y\text{ stabilises }|i\rangle
&\qquad-Y\text{ stabilises }|-i\rangle
\\X\text{ stabilises }|+\rangle
&\qquad-X\text{ stabilises }|-\rangle
\end{aligned}
where |\pm i\rangle=\frac{1}{\sqrt{2}}(|0\rangle\pm i|1\rangle) and |\pm\rangle=\frac{1}{\sqrt{2}}(|0\rangle\pm|1\rangle).
On the Bloch sphere, these single-qubit stabiliser states lie at the intersection of the three axes with the surface of the sphere.
We can also say something about the remaining two elements of the single-qubit Pauli group: \mathbf{1} stabilises everything, and -\mathbf{1} stabilises nothing (except for the zero state, which we explicitly ignore).
More generally, if S stabilises something then -S cannot stabilise the same thing.
The set of all stabilisers of a given state or given subspace form a group: if S|\psi\rangle=|\psi\rangle, then multiplying both sides by S^{-1} shows that the inverse of a stabiliser is again a stabiliser; the composition of two stabilisers is again a stabiliser, since (ST)|\psi\rangle=S(T|\psi\rangle)=S|\psi\rangle=|\psi\rangle; and as we have just said, the identity is always a stabiliser.
This group is called the stabiliser group \mathcal{S} of the given state or subspace.
Using this language, we can rephrase the previous example by saying that the stabiliser group of the state |0\rangle is \{\mathbf{1},Z\}=\langle Z\rangle, the stabiliser group of the state |1\rangle is \{\mathbf{1},-Z\}=\langle -Z\rangle, the stabiliser group of the state |+\rangle is \{\mathbf{1},X\}=\langle X\rangle, and so on.
If we take the tensor product of two states, with stabiliser groups \mathcal{A} and \mathcal{B} (respectively), then the resulting tensor product state has stabiliser group given by the cartesian product \mathcal{A}\times\mathcal{B}.
For example, the state |1\rangle|+\rangle is stabilised by the group
\begin{aligned}
\{\mathbf{1},Z\}\times\{\mathbf{1},X\}
&= \{\mathbf{1}\mathbf{1},\mathbf{1}X,Z\mathbf{1},ZX\}
\\&= \langle Z\mathbf{1},\mathbf{1}X\rangle.
\end{aligned}
As for the state |0\rangle^{\otimes n}, this is stabilised by the group generated by the n elements Z\mathbf{1}\mathbf{1}\ldots\mathbf{1}, \mathbf{1}Z\mathbf{1}\ldots\mathbf{1}, …, \mathbf{1}\mathbf{1}\ldots,Z, so we often simply stack the generators and write such generating sets as (n\times n) matrices, labelling the left-hand side with the relevant signs:
|0000\rangle
\longleftrightarrow
\begin{array}{c|cccc|}
+&Z&\mathbf{1}&\mathbf{1}&\mathbf{1}
\\+&\mathbf{1}&Z&\mathbf{1}&\mathbf{1}
\\+&\mathbf{1}&\mathbf{1}&Z&\mathbf{1}
\\+&\mathbf{1}&\mathbf{1}&\mathbf{1}&Z
\end{array}
and we can see that the signs determine the bit value in the computational basis state, if we look at the generators of the stabiliser groups for some other states:
|0001\rangle
\longleftrightarrow
\begin{array}{c|cccc|}
+&Z&\mathbf{1}&\mathbf{1}&\mathbf{1}
\\+&\mathbf{1}&Z&\mathbf{1}&\mathbf{1}
\\+&\mathbf{1}&\mathbf{1}&Z&\mathbf{1}
\\-&\mathbf{1}&\mathbf{1}&\mathbf{1}&Z
\end{array}
\qquad
|0101\rangle
\longleftrightarrow
\begin{array}{c|cccc|}
+&Z&\mathbf{1}&\mathbf{1}&\mathbf{1}
\\-&\mathbf{1}&Z&\mathbf{1}&\mathbf{1}
\\+&\mathbf{1}&\mathbf{1}&Z&\mathbf{1}
\\-&\mathbf{1}&\mathbf{1}&\mathbf{1}&Z
\end{array}
For our purposes, we are only really interested in stabilisers that are also elements of the n-qubit Pauli group \mathcal{P}_n, and we shall soon see that these form an abelian group.
It turns out that such stabilisers can describe highly entangled states.
In particular, the four Bell states (which we first talked about in Section 5.7) can be defined rather succinctly by their stabiliser groups:
| \Phi^+=|00\rangle+|11\rangle |
\langle XX,ZZ\rangle |
| \Psi^+=|01\rangle+|10\rangle |
\langle XX,-ZZ\rangle |
| \Phi^-=|00\rangle-|11\rangle |
\langle -XX,ZZ\rangle |
| \Psi^-=|01\rangle-|10\rangle |
\langle -XX,-ZZ\rangle |
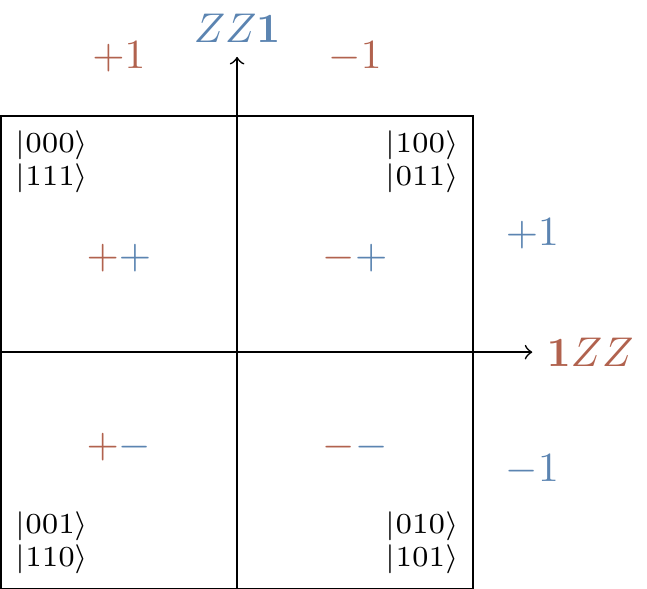
Not only this, but some vector spaces are also rather easily defined: the subspace of the three-qubit state space spanned by |000\rangle and |111\rangle is stabilised by
\{\mathbf{1}\mathbf{1}\mathbf{1},ZZ\mathbf{1},Z\mathbf{1}Z,\mathbf{1}ZZ\} = \langle ZZ\mathbf{1},\mathbf{1}ZZ\rangle.
Right now, it might seem more complicated to use stabilisers to define vectors or subspaces, but when we start looking at states with a larger and larger number of components we will see how this approach ends up being very tidy indeed!
It is not be true that the stabiliser description of states and subspaces will always be the most concise, but it is true in a lot of cases that are of interest to us.
Returning to our claim that stabiliser groups that are subgroups of \mathcal{P}_n are abelian, let us start with a definition, and then justify it afterwards.
An n-qubit Pauli stabiliser group is any subgroup of \mathcal{P}_n that is abelian and does not contain -\mathbf{1}.
Its elements are called Pauli stabilisers.
Recall that, in order for the subspace V_\mathcal{S} stabilised by some group \mathcal{S} to be non-trivial, we need -\mathbf{1}\not\in\mathcal{S}.
Given that all Pauli operators square to the identity, and all pairs of Pauli operators either commute or anticommute, this implies that if we want some Pauli operators to stabilise anything then they must commute.
Indeed, if S_1 and S_2 are two Pauli operators that anticommute, and |\psi\rangle is any vector stabilised by both of them, then
\begin{aligned}
|\psi\rangle
&= S_1S_2|\psi\rangle
\\&= -S_2S_1|\psi\rangle
\\&= -|\psi\rangle
\end{aligned}
which means that |\psi\rangle=0.
But saying that we are looking at a stabiliser group consisting of Pauli stabilisers that all commute with one another (as opposed to anticommuting) is exactly saying that we have an abelian subgroup of \mathcal{P}_n; if we want it to be non-trivial, then we need it to not contain -\mathbf{1}.
Conversely, if we pick any abelian subgroup of \mathcal{P}_n that does not contain -\mathbf{1}, this stabilises some subspace V_\mathcal{S}.
The size of any Pauli stabiliser \mathcal{S} is |\mathcal{S}|=2^r, where r is some positive integer, since we can always find some choice of generators G_1,\ldots,G_r, and then any operator S\in\mathcal{S} can be written as
S = G_1^{\epsilon_1}G_2^{\epsilon_2}\ldots G_r^{\epsilon_r}
where r_i\in\{0,1\}.
But given any stabiliser group, we can always express its elements using many different sets of generators; a specific choice of r independent generators of a Pauli stabiliser \mathcal{S} of size 2^r is called a presentation.
In order to choose a presentation from the set of elements of \mathcal{S}, we have to start by picking any non-identity element, of which there are 2^r-1.
Inductively then, we pick the next generator by picking any element which is not in the subgroup generated by the previously selected generators, which means that there are
(2^r-1)(2^r-2)(2^r-2^2)\ldots(2^r-2^{r-1})
possible generating sets of \mathcal{S}.
But these are ordered sets (i.e. we are keeping track of the order in which we pick the elements, so G_1,G_2,\ldots is a “different” choice than G_2,G_1,\ldots), so if we want to know the number of presentations then we can simply divide the expression above by r!.
For example, the Bell state \Phi^+=|00\rangle+|11\rangle is stabilised by the group \{\mathbf{1}\mathbf{1},XX,-YY,ZZ\}.
This stabiliser group has (2^2-1)(2^2-2)/2!=3 presentations, namely \langle XX,ZZ\rangle, \langle -YY,XX\rangle, and \langle ZZ,-YY\rangle.
So now we know the size of a Pauli stabiliser, but what can we say about the dimension of the subspace that it stabilises?
If |\mathcal{S}|=2^r then the corresponding stabiliser subspace V_\mathcal{S} has dimension 2^{n-r} (where n is the number of qubits, i.e. such that \mathcal{S}\subseteq\mathcal{P}_n).
To see this, we can look at the projector P_S onto V_\mathcal{S}, since once we have a projector onto any subspace we know that the dimension of that subspace is exactly the trace of the projector (we can prove this by thinking about the matrix of the projector in the diagonal form).
In our case (using the result of Exercise 7.8.5) we calculate that
\begin{aligned}
\operatorname{tr}P_S
&= \operatorname{tr}\frac{1}{2^r}(S_1+S_2+\ldots+S_{2^r})
\\&= \frac{1}{2^r}(\operatorname{tr}\mathbf{1})
\\&= 2^{n-r}
\end{aligned}
since any non-identity element of the stabiliser group has trace equal to zero, and \operatorname{tr}\mathbf{1}^{\otimes n}=2^n, whence \dim V_s=2^{n-r}.
If r=n then the stabilised subspace is 1-dimensional, and so we have stabiliser states.
There is a more geometric way of understanding why powers of 2 keep on turning up in these calculations.
Given independent Pauli generators, it is convenient to think about the state or subspace that they stabilise as being the result of repeatedly bisecting the Hilbert space.
Let G_1,\ldots,G_r be a presentation of a Pauli stabiliser \mathcal{S}.
For each operator G_i, half its eigenvalues are +1 and another half are -1, so each G_i bisects the 2^n-dimensional Hilbert space of n qubits into two eigenspaces of equal size.
So G_1 gives two 2^{n-1}-dimensional subspaces: one for the +1 eigenvalue and one for the -1 eigenvalue.
Forgetting about the -1 part and just focusing on the +1 part, G_2 then splits this 2^{n-1}-dimensional subspace into two 2^{n-2}-dimensional subspaces, since it is independent from G_1 (as we justify in Exercise 7.8.5).
Repeating this procedure, forgetting about the -1 subspace each time, leads us to consider the simultaneous +1-eigenspace of G_1,\ldots,G_r, where each time we pass from \{G_1,G_2,\ldots,G_i\} to \{G_1,G_2,\ldots,G_i,G_{i+1}\} we bisect the subspace into two equal parts once more, eventually ending with the 2^{n-2}-dimensional subspace V_\mathcal{S}, as above.
We can show this pictorially, as in Figure 7.1.
This diagram will make a reappearance in Sections 13 and 14.