Approximate phase estimation
In Section 10.8 we showed how to determine the phase of an eigenvalue of a controlled-U gate, hidden by an oracle, under the assumption that the phase was of a particularly nice rational form: 2\pi m/2^n.
More precisely, we were able to find the integer m\ \mathrm{mod}\ 2^n.
Here we will improve upon this result, explaining how to adapt the same circuit for arbitrary phases.
So say we have some controlled-U gate with eigenvector |u\rangle and eigenvalue e^{i\varphi}.
We can run the same circuit as we did in Section 10.8:
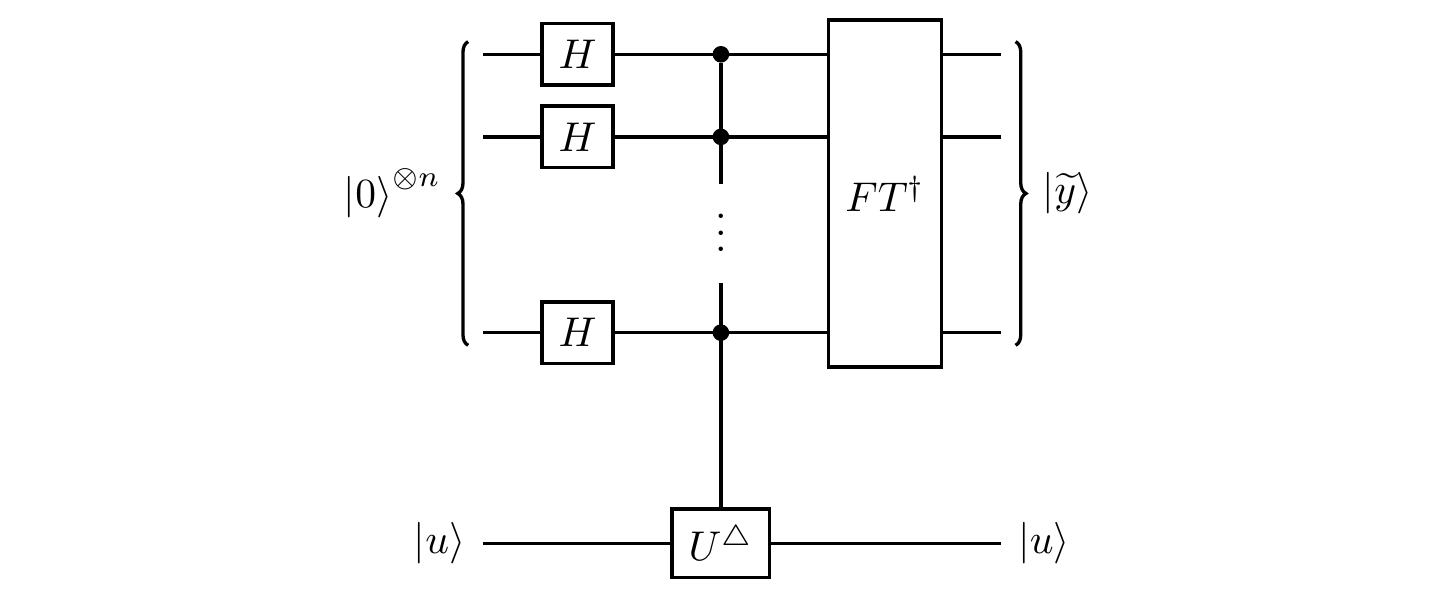
As before, the Hadamard gate followed by the controlled-U^\triangle gate prepare the state
\frac{1}{\sqrt{N}} \sum_{x=0}^{N-1} e^{i\varphi x}|x\rangle|u\rangle
where N=2^n, with n the number of qubits in the first register, since the phase kick-back leaves the eigenstate |u\rangle unchanged.
Now we apply the inverse quantum Fourier transform, giving
\frac{1}{N} \sum_{x,y=0}^{N-1} e^{ix(\varphi-2\pi y/N)}|y\rangle|u\rangle.
We already know that if N\varphi/2\pi has an exact n-bit representation (i.e. if \varphi=2\pi m/2^n with 0\leqslant m<N) then we are guaranteed to recover this when we measure the output |\widetilde{y}\rangle.
If this is not the case, then instead we can only hope for |\widetilde{y}\rangle to be the best n-bit approximation to N\varphi/2\pi.
This means that the distance between the two can be no more than 1/2 (otherwise |\widetilde{y}\rangle would round to N\varphi/2\pi\pm1 instead).
Rearranging this inequality gives
\left\vert\varphi-\frac{2\pi\widetilde{y}}{N}\right\vert
\leqslant\frac{\pi}{N}
which, if we define \delta=\varphi-2\pi\widetilde{y}/N, is exactly |\delta|\leqslant\pi/N.
Now we can calculate the probability of measuring the result |\widetilde{y}\rangle as
\begin{aligned}
p
&\coloneqq \frac{1}{N^2}\left\vert\sum_{x=0}^{N-1} e^{ix\delta}\right\vert^2
\\&= \frac{\sin^2(N\delta/2)}{N^2\sin^2(\delta/2)}.
\end{aligned}
Let’s see if we can find a lower bound for this probability.
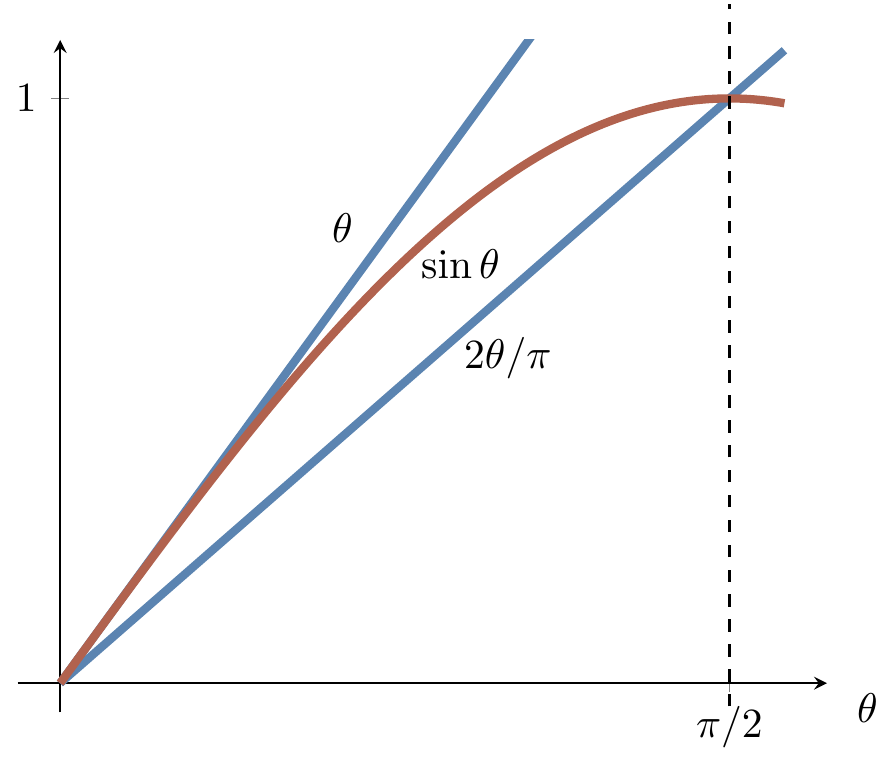
First of all, for small values of \theta, we know that \sin\theta<\theta.
In particular, \sin(\delta/2)<\delta/2.
Secondly, we can show that \sin(N\delta/2)>N\delta/\pi by using the fact that N\delta\leqslant\pi (though here we simply provide Figure 12.3 instead of giving a proof).
Thus
\begin{aligned}
p
&> \left(\frac{2N\delta}{N\delta\pi}\right)^2
\\&= \frac{4}{\pi^2} \approx 0.41
\end{aligned}
and so we find the best n-bit approximation to \varphi with pretty good probability.
In fact, the coefficients in these inequalities work in our favour: the further away a result |\widetilde{y}\rangle is from being the best n-bit approximation to \varphi, the lower our probability of measuring it.
This provides a way of getting good approximations with even higher probability, and one that we can choose ourselves, by using more qubits.
That is, if we increase the number of qubits in the first register to be t, for some t>n, then we know that with probability p=4/\pi^2 we will get the best t-bit approximation to \varphi.
But we’re only interested in the best n-bit approximation, and the 2^{t-n} next-most-likely outcomes — those that will truncate to give the same n-bit approximation — from the t-qubit circuit are all the next highest probability ones.
If one sums everything up carefully, then we can show that the probability of not measuring one of these is
\varepsilon
\leqslant\frac{1}{2(2^{t-n}-2)}
and so, for any desired \varepsilon, we get the best n-bit approximation with probability at least 1-\varepsilon by setting t to be
t
= n + \left\lceil\log_2\left(2+\frac{1}{2\varepsilon}\right)\right\rceil
(where \lceil x\rceil denotes the ceiling of x, i.e. the smallest integer larger than x).