Measuring Pauli stabilisers
How do we bisect Hilbert spaces in practice?
By measuring stabilisers.
Let’s start by measuring any single-qubit observable that squares to the identity.
The corresponding operator P with eigenvalues \pm1 is both Hermitian and unitary, and can thus represent both an observable and a quantum gate.
If we prepare a qubit in some state |\psi\rangle and then wish to perform a measurement that will give us a result of \pm1 and leave the qubit in a post-measurement state, namely the corresponding eigenvector, then we can use the following circuit (where \propto denotes that two states are multiples of one another).
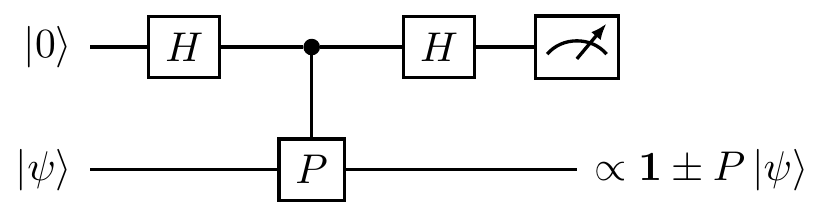
This construction requires an auxiliary qubit (in the top register), two Hadamard gates, and the tacit assumption that we can construct a controlled-P operator.
Stepping through the execution of this circuit, we get
\begin{aligned}
|0\rangle|\psi\rangle
&\overset{H\otimes\mathbf{1}}{\longmapsto}
\frac{1}{\sqrt{2}}(|0\rangle+|1\rangle)|\psi\rangle
\\&\overset{\texttt{c-}P}{\longmapsto}
\frac{1}{\sqrt{2}}|0\rangle|\psi\rangle + \frac{1}{\sqrt{2}}|1\rangle P|\psi\rangle
\\&\overset{H\otimes\mathbf{1}}{\longmapsto}
|0\rangle\frac{1}{2}(\mathbf{1}+P)|\psi\rangle + |1\rangle\frac{1}{2}(\mathbf{1}-P)|\psi\rangle.
\end{aligned}
The final state of the two qubits indicates that, when the auxiliary (top) qubit is found in state |0\rangle then we projected the state |\psi\rangle onto the +1-eigenspace of P (via the projector \frac{1}{2}(\mathbf{1}+P)), and when it is found in state |1\rangle then we projected |\psi\rangle onto the -1-eigenspace (via the projector \frac{1}{2}(\mathbf{1}-P)).
In particular, the X, Y, and Z observables can be measured using controlled-X, controlled-Y, and controlled-Z gates (respectively).
This pattern can easily be extended to an n-qubit Pauli operator.
For example, for n=3, a generic circuit that implements a projective measurement onto the \pm1-eigenspaces of S=P_1\otimes P_2\otimes P_3 has the form
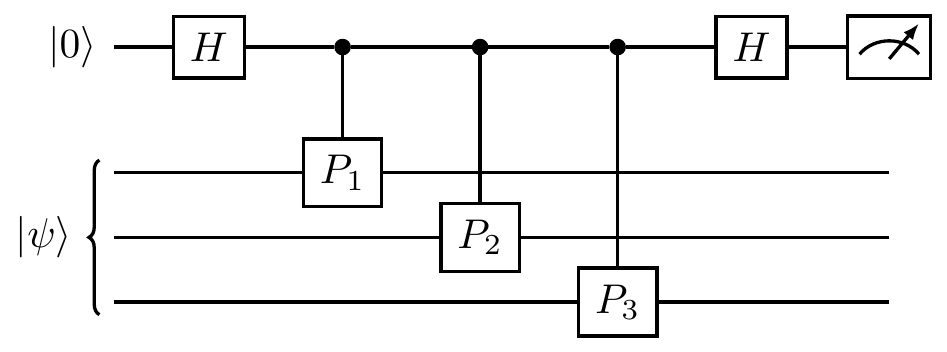
and is usually drawn more compactly as
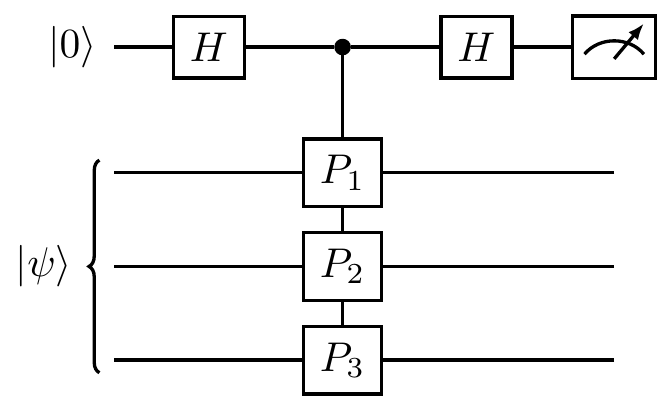
In this way, we can measure stabilisers and project onto the subspaces that they stabilise.
For example, take the stabiliser group \mathcal{S}=\langle XX,ZZ\rangle, and consider the circuit below:
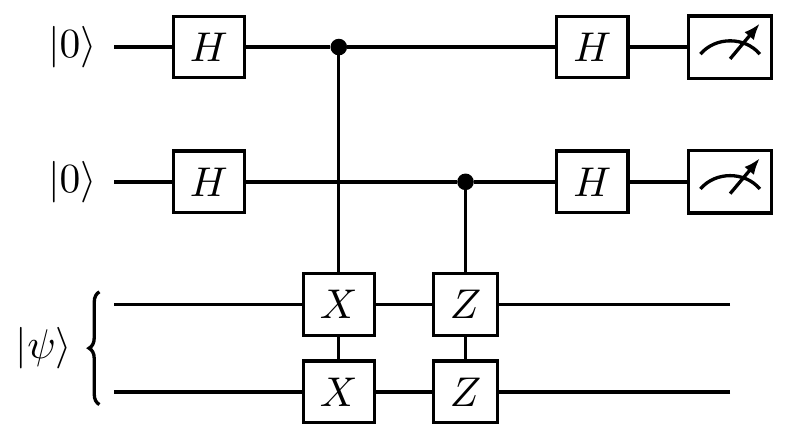
The registered bit values from the first and second (counting from the top) auxiliary qubits tell us how we bisect the Hilbert space with XX and ZZ (respectively), recalling that a bit value of 0 corresponds to the +1 Pauli eigenvalue, and a bit value of 1 to the -1 eigenvalue.
The first measurement can apply one of two projectors to |\psi\rangle:
- \frac{1}{2}(\mathbf{1}+XX), in which case the first auxiliary qubit will show 0, corresponding to the eigenvalue +1, and the subspace spanned by |00\rangle+|11\rangle and |01\rangle+|10\rangle
- \frac{1}{2}(\mathbf{1}-XX), in which case the first auxiliary qubit will show 1, corresponding to the eigenvalue -1, and the subspace spanned by |00\rangle-|11\rangle and |01\rangle-|10\rangle.
The second measurement can further project the resulting post-measurement state of the two qubits in one of two ways:
- \frac{1}{2}(\mathbf{1}+ZZ), in which case the second auxiliary qubit will show 0, corresponding to the eigenvalue +1, and the subspace spanned by |00\rangle+|11\rangle and |00\rangle-|11\rangle
- \frac{1}{2}(\mathbf{1}-ZZ), in which case the second auxiliary qubit will show 1, corresponding to the eigenvalue -1, and the subspace spanned by |01\rangle+|10\rangle and |01\rangle-|10\rangle.
So if both auxiliary qubits show bit value outcome 0 (corresponding to the Pauli outcome (+1,+1) of eigenvalues), then we have successfully projected onto the state stabilised by XX and ZZ, which is exactly |00\rangle+|11\rangle.
More generally, in Pauli notation, the outcome (\pm1,\pm1) corresponds to the projection onto the stabiliser state stabilised by \langle\pm XX,\pm ZZ\rangle.
Needless to say, we do not have any control over the actual outcomes of the measurement, but we do now know which post-measurement state we have generated.
This means that we can use the circuit to prepare a desired state by applying an appropriate unitary operation to the final state.
For example, if we want to generate the state |00\rangle+|11\rangle but actually end up with the state |00\rangle-|11\rangle, then we can simply apply the Z operation to any of the two qubits to get the desired result.
This generic method is not the only way of constructing projective measurements of Pauli observables, however — see Exercise 7.8.7



