Quantum bits, called “qubits”
Such a two-state machine that we have just described in abstract terms is usually realised as a controlled evolution of a two-state system, called a quantum bit, or qubit for short.
For example, the state |0\rangle may be chosen to be the lowest energy state of an atom (the ground state), and state |1\rangle a higher energy state (the excited state).
Pulses of light of the appropriate frequency, duration, and intensity can take the atom back and forth between the basis states |0\rangle and |1\rangle (implementing logical \texttt{NOT}).
Some other pulses (say, half the duration or intensity) will take the atom into states that have no classical analogue.
Such states are called coherent superpositions of |0\rangle and |1\rangle, and represent a qubit in state |0\rangle with some amplitude \alpha_0 and in state |1\rangle with some other amplitude \alpha_1.
This is conveniently represented by a state vector
|\psi\rangle =
\alpha_0|0\rangle + \alpha_1|1\rangle
\leftrightarrow
\begin{bmatrix}
\alpha_0
\\\alpha_1
\end{bmatrix}
By Born’s rule, we know that \alpha_0 and \alpha_1 cannot be arbitrary complex numbers: they must satisfy |\alpha_0|^2+|\alpha_1|^2=1.
This lets us draw the state vector “geometrically”, using the fact that the locus of vectors of magnitude equal to 1 describes a circle:
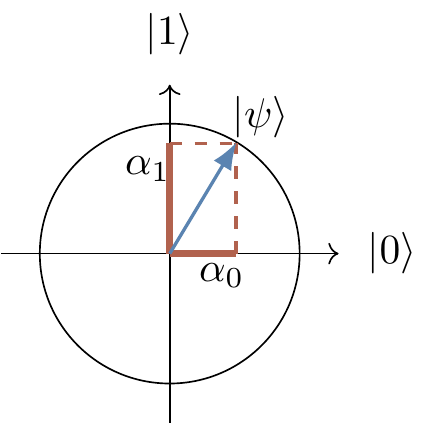
But recall that amplitudes are complex numbers, and so \alpha_0 and \alpha_1 cannot really be drawn as 1-dimensional real vectors on a flat screen or piece of paper;
the picture above provides good intuition, but to be fully accurate we would need to draw it in four-dimensional space (or at least on some three-dimensional paper).
A qubit is a quantum system in which the Boolean states 0 and 1 are represented by a prescribed pair of normalised and mutually orthogonal quantum states labelled by |0\rangle and |1\rangle.
The two states form a so-called computational (or standard) basis, and so any other state of an isolated qubit can be written as a coherent superposition
|\psi\rangle = \alpha_0|0\rangle + \alpha_1|1\rangle
for some \alpha_0 and \alpha_1 such that |\alpha_0|^2 + |\alpha_1|^2 = 1.
In practice, a qubit is typically a microscopic system, such as an atom, a nuclear spin, or a polarised photon.
As we have already mentioned, any computational step, that is, any physically admissible operation U on a qubit, is described by a (2\times 2) unitary matrix U.
It modifies the state of the qubit as
|\psi\rangle
\longmapsto
|\psi'\rangle
= U|\psi\rangle
which we can write explicitly as
\begin{bmatrix}
\alpha'_0
\\\alpha'_1
\end{bmatrix}
= \begin{bmatrix}
U_{00} & U_{01}
\\U_{10} & U_{11}
\end{bmatrix}
\begin{bmatrix}
\alpha_0
\\\alpha_1
\end{bmatrix}
That is, the operation U turns the state |\psi\rangle, with components \alpha_k, into the state |\psi'\rangle=U|\psi\rangle, with components \alpha'_l= \sum_k U_{lk}\alpha_k.

