5.6 Controlled-NOT

How do entangled states arise in real physical situations? The short answer is that entanglement is the result of interactions. It is easy to see that tensor product operations U_1\otimes\ldots\otimes U_n map product states to product states:

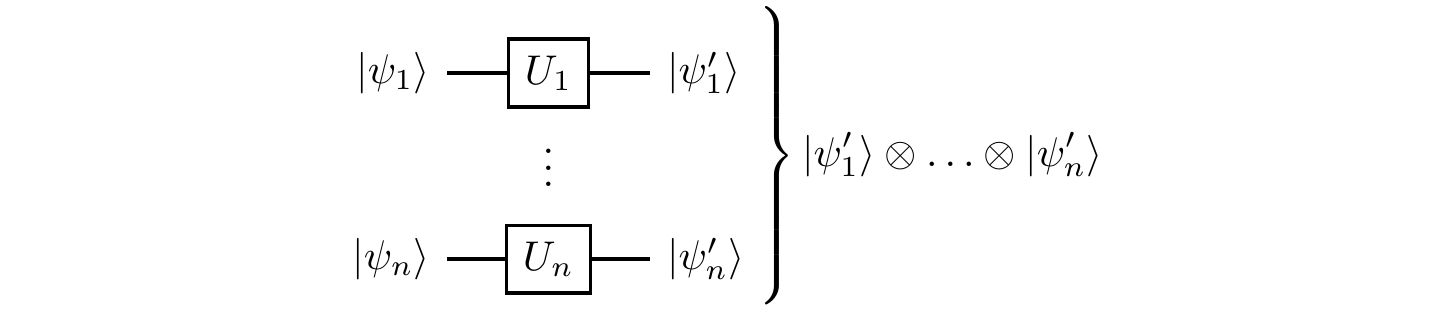
and so any collection of separable qubits remains separable. As soon as qubits start interacting with one another, however, they become entangled, and things start to get really interesting. We will describe interactions that cannot be written as tensor products of unitary operations on individual qubits.

The most popular two-qubit entangling gate is the controlled-\texttt{NOT} (or \texttt{c-NOT}), also known as the controlled-X gate.¹⁰⁸ The gate acts on two qubits: it flips the second qubit (referred to as the target) if the first qubit (referred to as the control) is |1\rangle, and does nothing if the control qubit is |0\rangle. In the standard basis \{|00\rangle,|01\rangle,|10\rangle,|11\rangle\}, it is represented by the following unitary matrix:

Controlled-\texttt{NOT}

\left[\begin{array}{c|c}\begin{matrix}1&0\\0&1\end{matrix}&\begin{matrix}0&0\\0&0\end{matrix}\\\hline\begin{matrix}0&0\\0&0\end{matrix}&\begin{matrix}0&1\\1&0\end{matrix}\end{array}\right]

We represent the \texttt{c-NOT} gate in circuit notation as shown in Figure 5.1.

Figure 5.1: Where x,y\in\{0,1\}, and \oplus denotes \texttt{XOR}, or addition modulo 2.

Note that this gate does not admit any tensor-product decomposition, but can be written as a sum of tensor products:¹⁰⁹ \texttt{c-NOT} = |0\rangle\langle 0|\otimes\mathbf{1}+ |1\rangle\langle 1|\otimes X (where X is the Pauli bit-flip operation).

The \texttt{c-NOT} gate lets us do many interesting things, and can act in a rather deceptive way. Let us now study some of these things.

---

108. Here, X\equiv\sigma_x refers to the Pauli operator that implements the bit-flip.↩︎

109. Make sure that you understand how the Dirac notation is used here. More generally, think why |0\rangle\langle 0|\otimes A + |1\rangle\langle 1|\otimes B means “if the first qubit is in state |0\rangle then apply A to the second one, and if the first qubit is in state |1\rangle then apply B to the second one”. What happens if the first qubit is in a superposition of |0\rangle and |1\rangle?↩︎