4.12 Remarks and exercises

4.12.1 Projector?

Consider two unit vectors |a\rangle and |b\rangle. Is the operator |a\rangle\langle a|+|b\rangle\langle b| a projector?

4.12.2 Knowing the unknown

Suppose you are given a single qubit in some entirely unknown quantum state |\psi\rangle=\alpha|0\rangle+\beta|1\rangle.

  1. Can you determine |\psi\rangle, using as many measurements as you want?

  2. Say you measure the qubit in the standard basis, and register outcome |0\rangle. What does this tell you about the pre-measurement state |\psi\rangle?

  3. How many real parameters do you need to determine |\psi\rangle? Would you be able to100 reconstruct |\psi\rangle from \langle\psi|X|\psi\rangle, \langle\psi|Y|\psi\rangle, and \langle\psi|Z|\psi\rangle?

  4. You are given zillions of qubits, all prepared in the same quantum state |\psi\rangle. How would you determine |\psi\rangle?

4.12.3 Measurement and idempotents

The Z measurement is defined by the projectors \begin{aligned} P_0 &= \frac{1}{2}(\mathbf{1}+ Z), \\P_1 &= \frac{1}{2}(\mathbf{1}- Z). \end{aligned} Let’s generalise this.

Consider the measurement associated to any Hermitian operator S that satisfies S^2=\mathbf{1}. Show that the two outcomes \pm1 correspond to the projectors \frac{1}{2}(\mathbf{1}\pm S).

4.12.4 Unitary transformations of measurements

In our quantum circuits, unless specified otherwise, all measurements are assumed to be performed in the standard basis. This is because any measurement can be reduced to the standard measurement by performing some prior unitary transformation.

  1. Show that101 any two orthonormal bases \{|e_1\rangle,\ldots,|e_n\rangle\} and \{|d_1\rangle,\ldots,|d_n\rangle\} are always related by some unitary U.

  2. Suppose that the projectors P_k define the standard measurement. Show that, for any unitary U, the projectors UP_kU^\dagger also define a measurement.

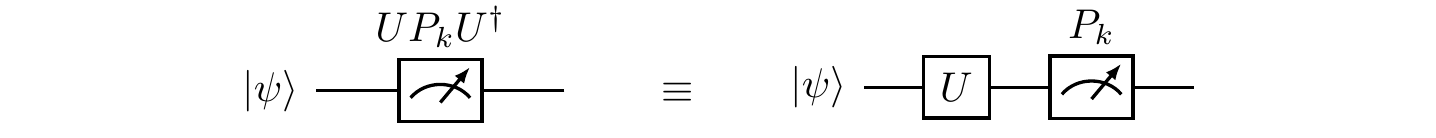
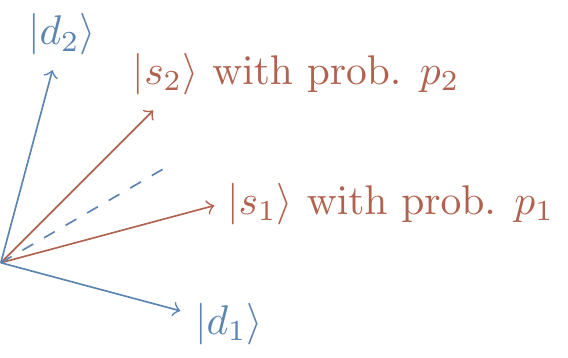
4.12.5 Optimal measurement

The optimal measurement to distinguish between the two equally likely non-orthogonal signal states, |s_1\rangle and |s_2\rangle, is described by the two orthogonal vectors |d_1\rangle and |d_2\rangle, placed symmetrically around the signal states, as we saw in Section 4.9. But suppose the states are not equally likely: say |s_1\rangle is chosen with probability p_1 and |s_2\rangle with probability p_2. How would you modify the measurement to maximise the probability of success in this case?

4.12.6 Alice knows what Bob did

Alice prepares a qubit in any state of her choosing and gives it to Bob, who secretly measures either \sigma_x or \sigma_y. The outcome of the measurement is seen only by Bob. Alice has no clue which measurement was chosen by Bob, but right after his measurement she gets her qubit back and she can measure it as well. Some time later, Bob tells Alice which of the two measurements was chosen, i.e. whether he measured \sigma_x or \sigma_y. Alice then tells him the outcome he obtained in his measurement. Bob is surprised, since the two measurements have mutually unbiased bases, and yet Alice always gets it right, no matter how many times they repeat the experiment. How does she do it?

This is a simplified version of a beautiful quantum puzzle proposed in 1987 by Lev Vaidman, Yakir Aharonov, and David Z. Albert in a paper with the somewhat provocative title “How to ascertain the values of \sigma_x, \sigma_y, and \sigma_z of a spin-\frac{1}{2} particle”. For the original, see Phys. Rev. Lett. 58 (1987), p. 1385.

4.12.7 The Zeno effect

  1. Hint: it may help you to visualise |\psi\rangle as a Bloch vector.↩︎

  2. Hint: it suffices to show that \sum_k |d_k\rangle\langle e_k| is unitary — why?↩︎