9.7 Composition of quantum channels

We mentioned that quantum channels are combinations of

  1. adding a physical system in a fixed state (via tensoring),
  2. unitary transformations, and
  3. discarding a physical system (taking a partial trace).

As expected from the fact that the Stinespring point of view is equivalent to the Kraus point of view, each of these operations admits an operator-sum decomposition. This is obvious for unitary evolution (\rho\mapsto U\rho U^\dagger), but perhaps less so for the other two operations. One reason to care about this is that the Kraus decomposition gives a tidy way of describing composition of quantum channels.

  • Adding a system. Any quantum system can be expanded by bringing in an auxiliary system in a fixed state |a\rangle. This transformation takes vectors in the Hilbert space associated with the original system and tensors them with a fixed vector |a\rangle in the Hilbert space associated with the auxiliary system: |\psi\rangle \longmapsto |a\rangle\otimes|\psi\rangle = (|a\rangle\otimes\mathbf{1}) |\psi\rangle. In terms of density operators, we write this “expansion” transformation as \begin{aligned} \rho \longmapsto \rho' &= |a\rangle\langle a|\otimes\rho \\&= (|a\rangle\otimes\mathbf{1})\rho (\langle a|\otimes\mathbf{1}) \\&= V\rho V^\dagger \end{aligned} where V=|a\rangle\otimes\mathbf{1}. We note that V^\dagger V=\langle a|a\rangle\otimes\mathbf{1}=\mathbf{1} is the identity in the Hilbert space associated with the system, and so V is an isometry. Indeed, this transformation is an isometric embedding.

  • Discarding a system. Conversely, given a composite system in state \rho, we can discard one of its subsystems. The partial trace over an auxiliary system can be written in the Kraus representation as \begin{aligned} \rho \longmapsto \rho' &= \operatorname{tr}_\mathcal{A}\rho \\&= (\operatorname{tr}\otimes\mathbf{1})\rho \\&= \sum_i (\langle i|\otimes\mathbf{1})\rho(|i\rangle\otimes\mathbf{1}) \\&= \sum_i E_i\rho E^\dagger_i \end{aligned} where the vectors |i\rangle form an orthonormal basis in the Hilbert space associated with the auxiliary system. Again, we can check that the Kraus operators E_i=|i\rangle\otimes\mathbf{1} satisfy the completeness relation \sum_i E^\dagger_i E_i =\mathbf{1}\otimes\mathbf{1} (using the fact that \sum_i|i\rangle\langle i|=\mathbf{1}).

Any sequential composition of two quantum channels \mathcal{E} and \mathcal{F} with Kraus operators \{A_i\}_{i\in I} and \{B_j\}_{j\in J} (respectively) is another quantum channel183 described by the Kraus operators \{B_jA_i\}_{i\in I,j\in J}. Showing this is rather straightforward, at least in the operator-sum representation: let \begin{aligned} \mathcal{E} &= \sum_i A_i\cdot A^\dagger_i \\\mathcal{F} &= \sum_j B_j\cdot B^\dagger_j \end{aligned} where \sum_i A^\dagger_i A_i=\sum_j B^\dagger_j B_j=\mathbf{1}; then the sequential composition of \mathcal{E} followed by \mathcal{F} can be written as \mathcal{F} \circ\mathcal{E} = \sum_{i,j} (B_jA_i) \cdot (B_jA_i)^\dagger so that the B_jA_i are the Kraus operators associated with the new channel \mathcal{F}\circ\mathcal{E}, where the normalisation condition (or completeness relation) follows from \begin{aligned} \sum_{i,j} (B_jA_i)^\dagger (B_jA_i) &= \sum_i A_i^\dagger\left(\sum_j B_j^\dagger B_j\right)A_i \\&= \sum_i A_i^\dagger A_i \\&= \mathbf{1}. \end{aligned}

You might wonder why we explicitly called the above composition “sequential” — isn’t this how we always compose functions? In actual fact, since we have access to tensor products, there is another sort of composition, namely parallel184 composition: if we have systems \mathcal{A} and \mathcal{B} with channels \mathcal{E}_\mathcal{A} acting on \mathcal{A} and \mathcal{E}_\mathcal{B} acting on \mathcal{B}, then the parallel composition is denoted by \mathcal{E}_\mathcal{A}\otimes\mathcal{E}_\mathcal{B}, acting on the joint system \mathcal{A}\otimes\mathcal{B}, and with Kraus operators given by the A_i\otimes B_j. The normalisation condition again follows from a simple calculation: \begin{aligned} \sum_{i,j} (A_i\otimes B_j)^\dagger (A_i\otimes B_j) &= \sum_{i,j} A_i^\dagger A_i \otimes B_j^\dagger B_j \\&= \mathbf{1}_A\otimes\mathbf{1}_B. \end{aligned}

Now that we know how to compose quantum channels in terms of Kraus operators, we can see that the Stinespring representation is perfectly consistent with the Kraus representation: the three basic operations that we are allowed to use to build channels in the Stinespring representation (i.e. adding a system, unitary evolution, and discarding a system) are all themselves quantum channels, in that they admit a Kraus decomposition.

Before moving on, we make a small (but important) remark:

When we compose quantum channels, each channel needs its own independent ancilla — do not share ancillas between different channels.

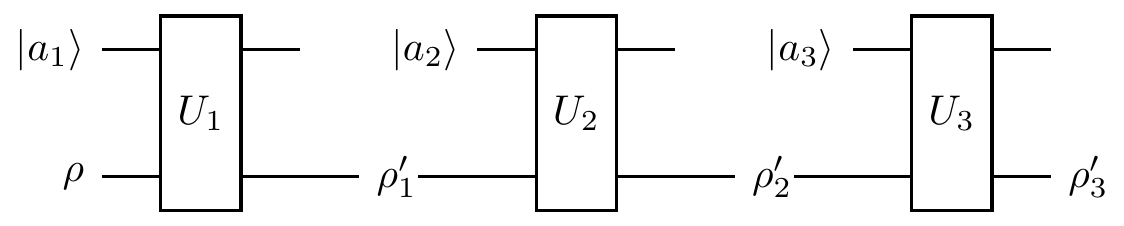
For example, say we have three channels, \mathcal{E}_1, \mathcal{E}_2, and \mathcal{E}_3, with \mathcal{E}_i defined by the unitary U_i and the state |a_i\rangle of its ancilla. Then the (sequential) composition \mathcal{E}_3\circ\mathcal{E}_2\circ\mathcal{E}_1 is given by

where each \mathcal{E}_i has its own associated ancilla |a_i\rangle. For more on this, see Section 9.12.2, where we talk about Markov approximation.

  1. Here we have tacitly assumed that the dimensions agree, i.e. that the output of \mathcal{E} and the input of \mathcal{F} are of the same dimension, so that the composition makes sense.↩︎

  2. You might also call this simultaneous composition, to contrast with sequential composition, but “parallel” is by far the most commonly accepted terminology.↩︎