2.5 The square root of NOT

Now that we have poked our heads into the quantum world, let us see how quantum interference challenges conventional logic. Consider the following task:

Design a logic gate that operates on a single bit and such that when it is followed by another, identical, logic gate the output is always the negation of the input.

Let us call the resulting logic gate the square root of \texttt{NOT}, or \sqrt{\texttt{NOT}}.

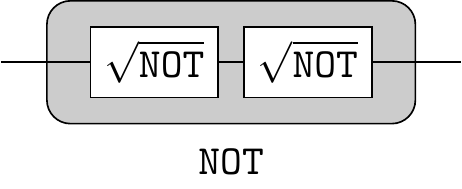
A simple check, such as an attempt to construct a truth table, should persuade you that there is no such operation in logic. It may seem reasonable to argue that since there is no such operation in logic, \sqrt{\texttt{NOT}} is impossible. But it does exist! Experimental physicists routinely construct such “impossible” gates in their laboratories. It is a physically admissible operation described by the unitary matrix⁵² \sqrt{\texttt{NOT}} = \frac{1}{2} \begin{bmatrix} 1+i & 1-i \\1-i & 1+i \end{bmatrix} = \frac{1}{\sqrt{2}} \begin{bmatrix} e^{i\frac{\pi}{4}} & e^{-i\frac{\pi}{4}} \\e^{-i\frac{\pi}{4}} & e^{i\frac{\pi}{4}} \end{bmatrix}. Indeed, \frac{1}{2} \begin{bmatrix} 1+i & 1-i \\1-i & 1+i \end{bmatrix} \frac{1}{2} \begin{bmatrix} 1+i & 1-i \\1-i & 1+i \end{bmatrix} = \begin{bmatrix} 0&1 \\1&0 \end{bmatrix}.

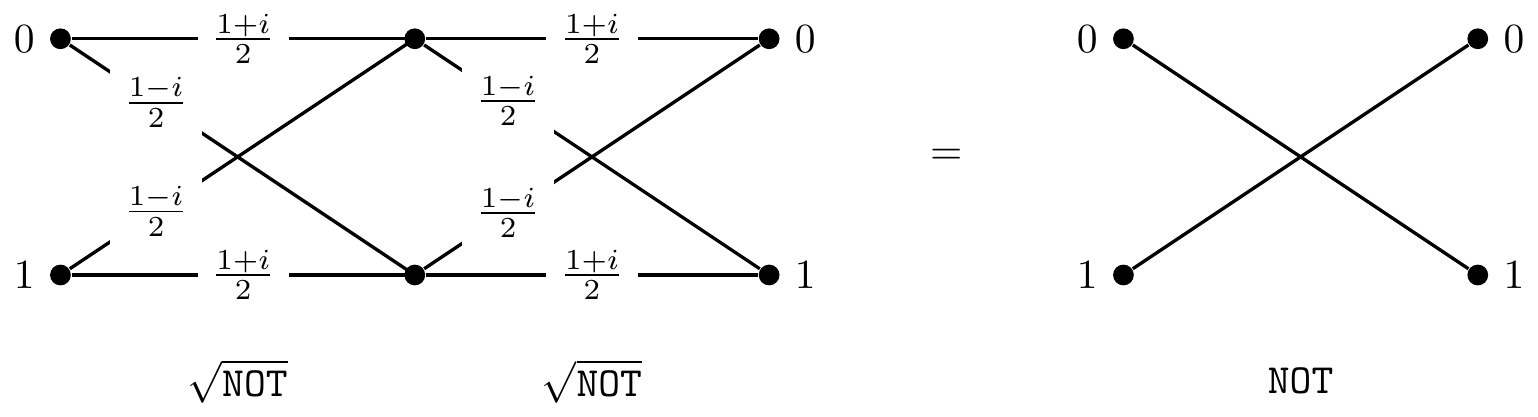
$A computation that, when repeated, gives exactly \texttt{NOT}. An unlabelled line means that it has probability 1, and the lack of a line corresponds to having probability 0.$

Figure 2.2: A computation that, when repeated, gives exactly \texttt{NOT}. An unlabelled line means that it has probability 1, and the lack of a line corresponds to having probability 0.

We could also step through the circuit diagram and follow the evolution of the state vector:

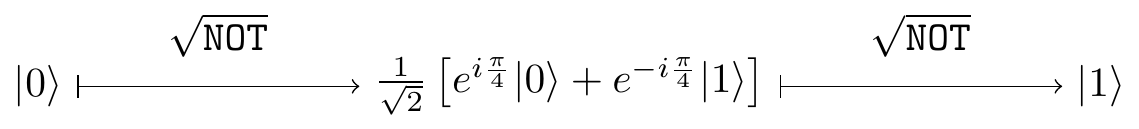
Or, if you prefer to work with column vectors and matrices, you can write the two consecutive application of \sqrt{\texttt{NOT}} to state |0\rangle as⁵³ \begin{bmatrix}0\\1\end{bmatrix} \,\longleftarrow\!\!\!\vert\,\, \frac{1}{\sqrt{2}} \begin{bmatrix} e^{i\frac{\pi}{4}} \\e^{-i\frac{\pi}{4}} \end{bmatrix} \,\longleftarrow\!\!\!\vert\,\, \begin{bmatrix}1\\0\end{bmatrix} where each “\longleftarrow\!\!\!\vert” denotes multiplication by \frac{1}{\sqrt{2}}\begin{bmatrix}e^{i\frac{\pi}{4}}&e^{-i\frac{\pi}{4}}\\e^{-i\frac{\pi}{4}}&e^{i\frac{\pi}{4}}\end{bmatrix}.

One way or another, quantum theory explains the behaviour of \sqrt{\texttt{NOT}}, and so, reassured by the physical experiments⁵⁴ that corroborate this theory, logicians are now entitled to propose a new logical operation \sqrt{\texttt{NOT}}. Why? Because a faithful physical model for it exists in nature!

There are infinitely many unitary operations that act as the square root of \texttt{NOT}.↩︎
Just remember that circuits diagrams are read from left to right, and vector and matrix operations go from right to left.↩︎
One such experiment (which we will soon discuss, in Section 3.1) is the so-called Mach-Zehnder interferometer.↩︎