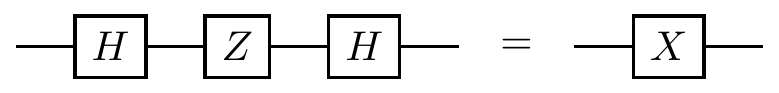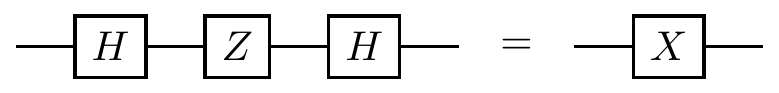From bit-flips to phase-flips, and back again
The Pauli Z gate is a special case of a phase gate P_\varphi with \varphi=\pi.
When we insert it into the interference circuit we obtain
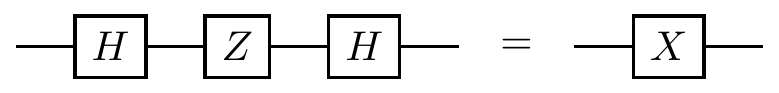
If you wish to verify this, write the Hadamard gate as H = (X+Z)/\sqrt{2} and use the properties of the Pauli operators.
So the Hadamard gate turns phase-flips into bit-flips, but it also turns bit-flips into phase-flips:

Let us also add, for completeness, that HYH=-Y.
You will see these identities again and again, especially when we discuss quantum error corrections.
\begin{aligned}
HXH &= Z
\\HZH &= X
\\HYH &= -Y
\end{aligned}