13.2 Towards error correction
In Section 13.1, when Alice used a random choice of four isometries to produce a three-qubit output, notice how we can write
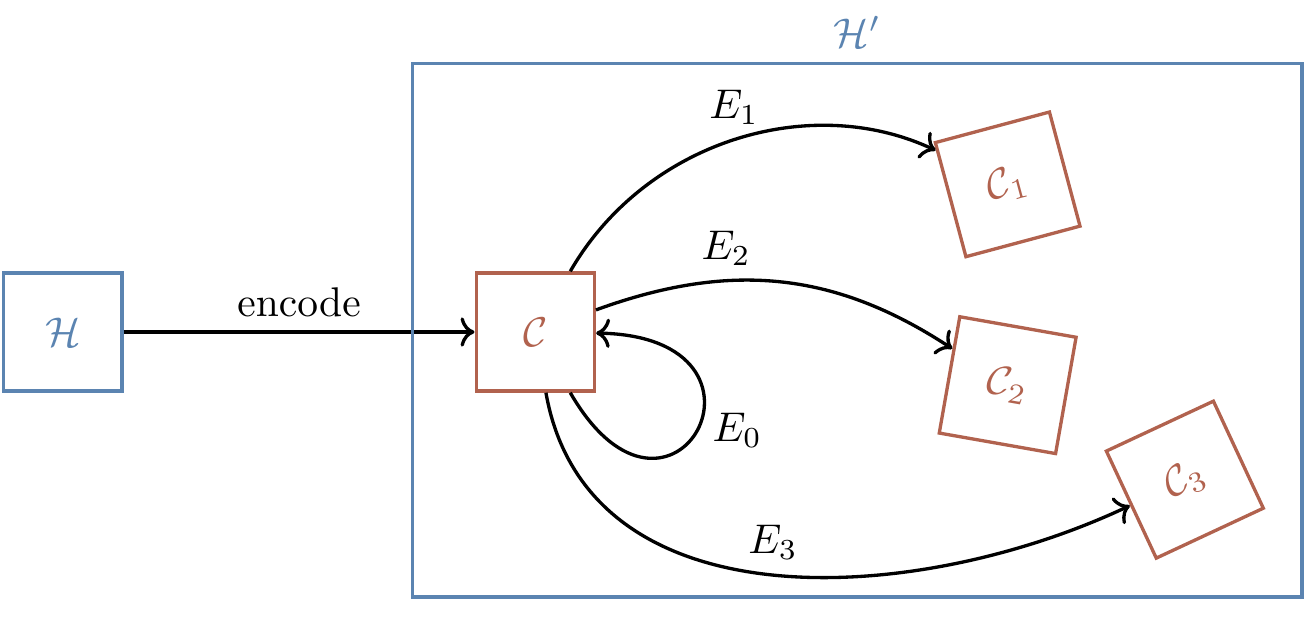
Correcting the isometry then corresponds to identifying which error happened, fixing it, and then removing the encoding: a process known as decoding. This is the format of error correction in a nutshell.
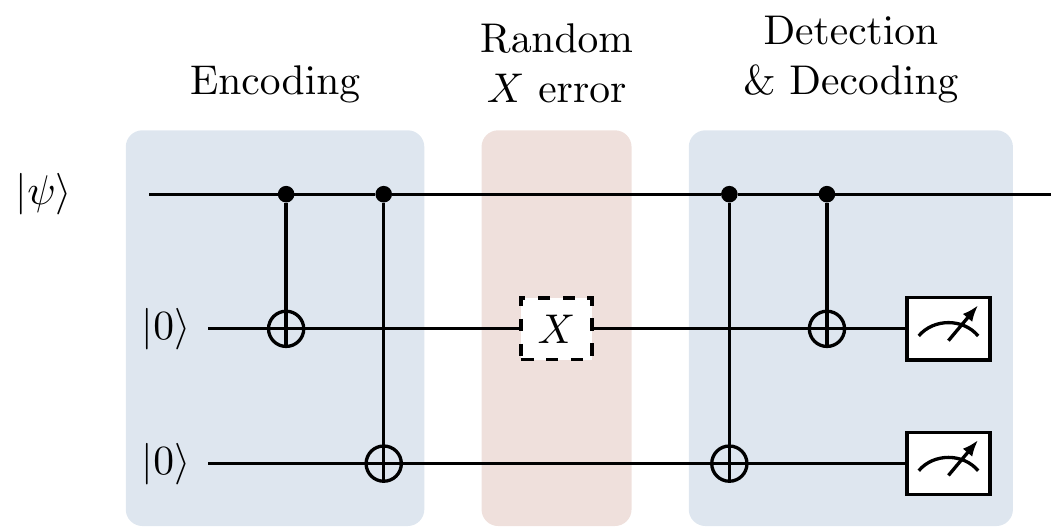
Figure 13.2: Quantum error correction can be thought of as a three-step process: encoding, transmitting through a noisy channel, and then detecting and decoding. We will give a more accurate depiction of an error correcting diagram, explaining what actually happens in the “detection & decoding portion” in Figure 13.7.
When we studied Pauli stabilisers in Section 7.2, we came across exactly the spaces of this example:
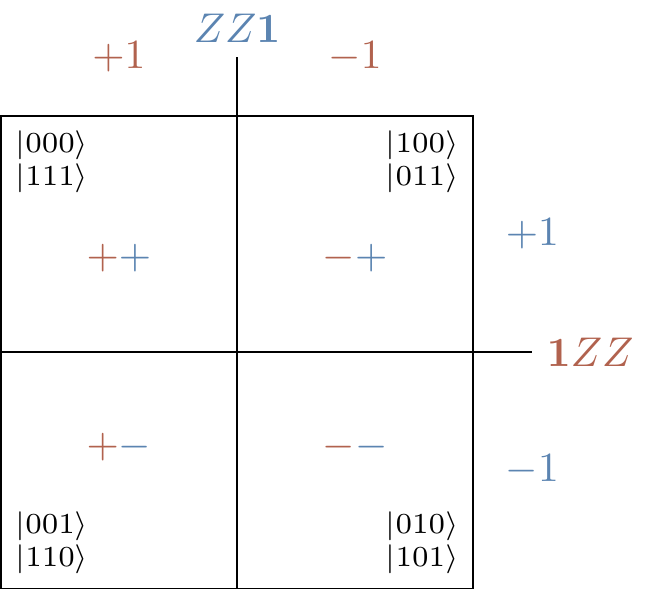
The stabiliser formalism gives us a very natural way of describing the error correcting code, along with its correction:
- the codespace (i.e. the space with no error) is defined by the two stabilisers
+ZZ\mathbf{1} and+\mathbf{1}ZZ - the error can be determined by measuring the value of these two stabilisers; we simply have to find which of the four possible errors gives the correct (anti-)commutation relations as specified by the measurement outcomes
\pm1 .
Generalising this idea further is the subject of Section 13.6.
If a set